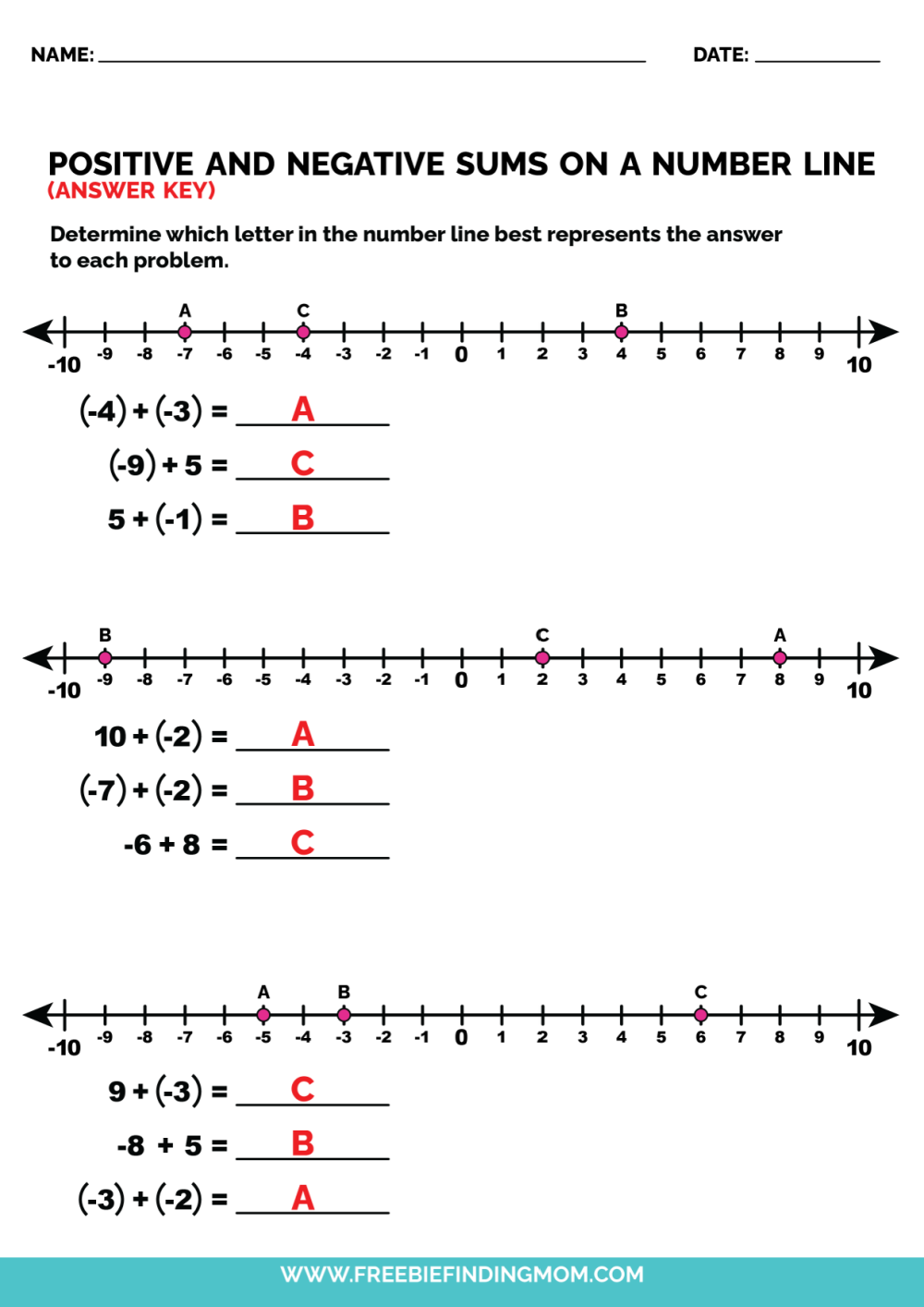
5 Ways to Master Number Lines: Positive and Negative Numbers

Mastering number lines, especially when it comes to positive and negative numbers, is a fundamental skill in mathematics that not only aids in understanding arithmetic but also provides a foundation for more complex mathematical concepts. Whether you're an educator, a student, or someone brushing up on math skills for personal development or work, this guide will walk you through five proven strategies to master number lines and navigate through both the positive and negative realms with ease.
1. Understanding the Basics of a Number Line

What is a Number Line?
- A number line is a straight line on which numbers are marked at evenly spaced intervals, typically representing integers. It serves as a visual tool to help understand the order and distance between numbers.
Positive and Negative Numbers:
- On a number line, positive numbers are usually to the right of zero, while negative numbers are to the left. Zero itself is considered neither positive nor negative.
Here's how a basic number line might look:
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |

Tips for Understanding:

- Visualize zero as the dividing point.
- Move to the right to add or for positive operations, and left for subtraction or negative operations.
💡 Note: Always ensure that you have a clear understanding of zero's position on the number line as it anchors the entire concept of positive and negative numbers.
2. Using Number Line Visuals for Addition and Subtraction

Addition:
- To add numbers, start at one point on the number line and move to the right for positive numbers or left for negative numbers.
Subtraction:
- Subtracting is essentially adding the opposite; move left for subtracting a positive number or right when subtracting a negative number.
Examples:

- Adding 3 to -2: Start at -2, move 3 units to the right to land on 1.
- Subtracting -5 from 4: Start at 4, move 5 units to the right (because subtracting a negative is like adding) to land on 9.
Implementing this visual strategy in practice can greatly aid in understanding the abstract concept of operations with signed numbers.
3. Incorporating Number Lines into Multiplications and Divisions

Multiplication and division on a number line can be a bit more abstract, but visual aids can help:
- Multiplication: Think of multiplication as repeated addition. If you multiply by 2, you'll move twice the distance of your starting point. Positive numbers move right, negatives move left.
- Division: Division involves understanding how many times one number fits into another. It helps to visualize this by segmenting the number line into equal parts.
Example:

- To multiply -2 by 3, you start at zero, move left by two units (the absolute value of -2), then do that three times to land at -6.
📝 Note: Visualizing multiplication and division on a number line helps cement the idea of direction and distance in arithmetic operations with negative numbers.
4. Applying Number Lines to Real-World Situations

Number lines aren’t just for classroom math; they’re applicable in everyday life:
- Temperature: Fahrenheit or Celsius scales can be visualized as a number line, with zero degrees as the dividing line.
- Altitude: Sea level can be considered zero, with elevations above being positive and below being negative.
- Finances: Think of income as positive and expenses or debts as negative on a number line.
Practical Application:

- If you’re climbing a mountain, your elevation change can be tracked using a number line, where every 100 meters climbed could be a step to the right, and every 100 meters descended, a step to the left.
5. Engaging with Interactive Tools and Games
The integration of technology has brought about a plethora of interactive tools and games that can make mastering number lines fun and engaging:
- Math Apps: Apps like Number Line by Mr. Nussbaum or DragonBox Numbers provide interactive learning environments.
- Online Games: Websites like Coolmath Games or ABCmouse offer games where children can practice number line navigation in a gamified context.
Benefits of Interactive Learning:

- Reinforces understanding through repetition in a playful setting.
- Allows for immediate feedback, helping to correct misunderstandings instantly.
- Keeps engagement high through the use of multimedia elements like animations and sound.
🎮 Note: Interactive tools and games can turn the sometimes dull practice of number line exercises into an enjoyable learning experience, particularly for younger learners.
In wrapping up this exploration of number lines, let's revisit the key points that can guide you towards mastering positive and negative numbers:
- Understand the basics of what a number line represents.
- Use visuals for addition and subtraction to solidify the concepts.
- Apply number lines to complex operations like multiplication and division for deeper comprehension.
- Relate number line usage to real-world scenarios to enhance its practicality.
- Leverage interactive tools and games to make learning both fun and effective.
Remember, mastering number lines isn't just about number crunching; it's about building a conceptual framework that can support a lifetime of mathematical understanding and application. Whether you're calculating stock market gains, managing personal finances, or simply helping a child with their homework, the mastery of number lines with positive and negative numbers will prove to be an invaluable skill.
Why is understanding number lines important?

+
Understanding number lines is fundamental as it helps conceptualize the relationship between numbers, aids in arithmetic operations, and provides a visual representation of mathematical concepts, making abstract ideas more tangible and easier to grasp.
How do negative numbers relate to real-life situations?

+
Negative numbers are used to denote various real-life situations like below-zero temperatures, elevations below sea level, financial debts, and time zones relative to Coordinated Universal Time (UTC).
Can you explain how to divide negative numbers using a number line?

+
To divide negative numbers using a number line, first determine how many times the divisor fits into the dividend in terms of distance. For instance, if you’re dividing -9 by -3, you start at zero and mark three negative steps, then repeat this process twice to get to the result of 3 (since -3 fits into -9 three times).