Master Points, Lines, Planes, and Angles Worksheet Answers

Geometry is a fascinating branch of mathematics that deals with the study of the shape, size, properties, and position of figures. For students and enthusiasts alike, mastering the basics of geometric concepts such as points, lines, planes, and angles is crucial. This blog post will delve into these fundamental concepts, offering explanations, examples, and the answers to common geometry worksheets, helping learners to enhance their understanding and apply their knowledge effectively.
Understanding Points

Let's begin with the simplest geometric concept:
Point: A point in geometry is the most basic unit of measurement. It represents a location in space and has no dimensions (length, width, or thickness). Points are typically represented with a dot and a label. Here's how they function in geometry:
- Representation: A point can be shown as a dot (•), with an uppercase letter such as A, B, or C.
- Characteristics: A point has a specific location but no size or shape.
📌 Note: Points are often used to locate vertices in polygons or define lines and planes.
Delving into Lines

A line extends indefinitely in both directions:
Line: Unlike a point, a line is a one-dimensional geometric figure that extends infinitely in both directions. Here are key aspects:
- Representation: Lines are usually named after any two points lying on them, using an arrow on both ends like this: AB↔.
- Properties: A line is straight with zero thickness, and it can have an infinite number of points.
- Types of Lines:
- Straight Line: A line that doesn't bend.
- Segment: A part of a line with two endpoints (AB).
- Ray: A line with one endpoint extending infinitely in one direction (AB).
Introducing Planes

The concept of a plane can be visualized as follows:
Plane: Planes are two-dimensional surfaces that extend infinitely in all directions. Here's what you need to know:
- Representation: Often represented by a simple two-dimensional figure, like a flat piece of paper, with a label like Plane M.
- Characteristics: A plane is flat, infinite, and has no thickness.
📍 Note: Any three non-collinear points determine a unique plane.
Exploring Angles
Angles add depth to geometric shapes:
Angles: An angle is formed when two rays share a common endpoint, known as the vertex. Here's a deeper look:
- Types of Angles:
Type Description Acute Angle Less than 90° Right Angle Exactly 90° Obtuse Angle Between 90° and 180° Straight Angle Exactly 180° Reflex Angle More than 180° but less than 360° 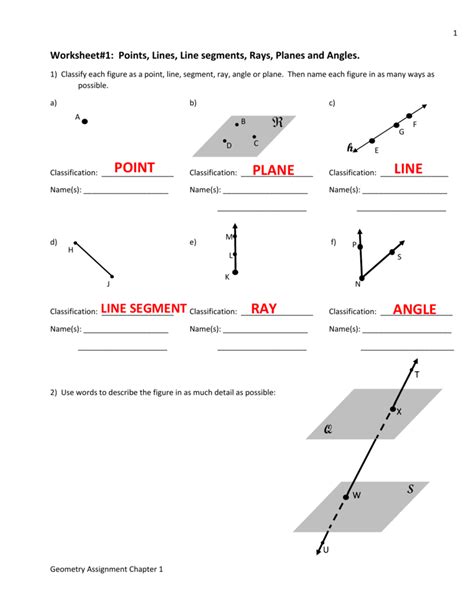
As you can see, geometry is filled with rich layers of concepts that build upon each other. Understanding these fundamental elements allows us to construct, analyze, and solve more complex problems in various fields of study.
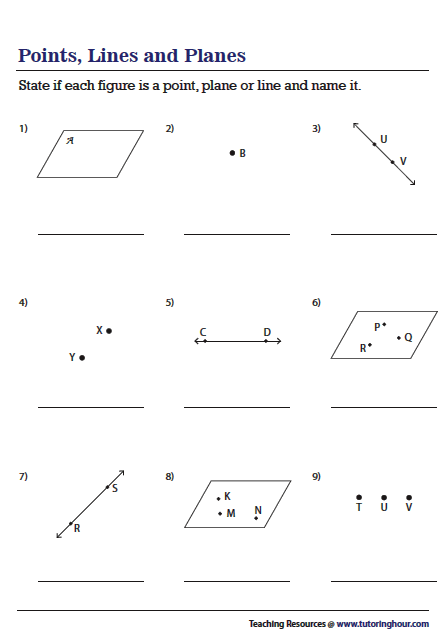
Worksheet Answers for Points, Lines, Planes, and Angles
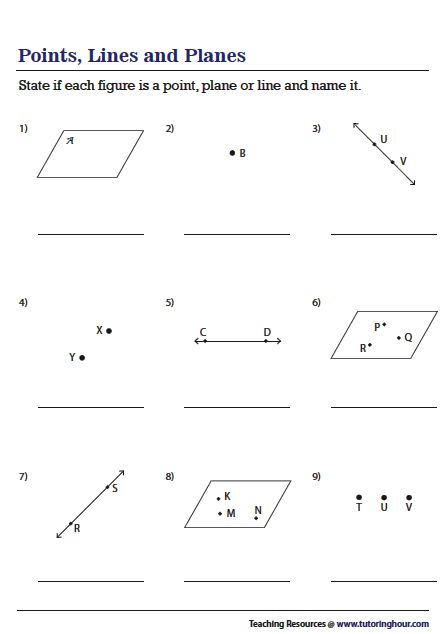
Let's provide some answers to common worksheet questions to reinforce your understanding:
- Identify Points, Lines, and Planes:
- Point A is a singular location with no dimensions.
- Line BC extends indefinitely in both directions.
- Plane DEF is represented by a flat surface extending infinitely.
- Determine the Type of Lines:
- Parallel lines: Two lines that do not intersect and are equidistant.
- Intersecting lines: Lines that cross at a single point.
- Perpendicular lines: Lines that intersect at a right angle (90°).
- Find the Measurement of Angles:
- An angle between two rays could be an acute, right, obtuse, straight, or reflex angle based on its degree measure.
- To find an angle's measure, use a protractor or known properties of specific shapes.
To summarize, mastering the fundamentals of geometry involves recognizing and understanding points, lines, planes, and angles. Each element builds upon the last, creating a foundation for further mathematical exploration. Whether you're solving a geometric proof or designing a piece of architecture, these basic concepts are your toolkit for navigating the spatial world. Remember that practice through worksheets and real-world applications will solidify these abstract ideas into concrete understanding.
What is the difference between a point and a line?

+
A point is a location with no dimensions, while a line is a one-dimensional object that extends infinitely in both directions.
How many points are needed to define a plane?

+
Any three non-collinear points determine a unique plane.
What are the different types of angles?

+
The types of angles include acute (less than 90°), right (exactly 90°), obtuse (between 90° and 180°), straight (exactly 180°), and reflex (more than 180° but less than 360°).



