Master Fraction to Decimal Conversion with Our Worksheet

"Mathematics is not about numbers, equations, computations, or algorithms: it is about understanding." – William Paul Thurston. This profound statement encapsulates the essence of why we delve into math topics like converting fractions to decimals. It's not just the manipulation of numbers but understanding the underlying principles and their real-life applications. In this comprehensive guide, we will journey through the intricacies of converting fractions into decimals using an interactive worksheet, ensuring not only that you grasp the math, but also how this knowledge applies to everyday scenarios.
Why Convert Fractions to Decimals?

Fractions and decimals represent parts of a whole, but they are used differently in various contexts. Here are some practical reasons for converting:
- Decimal Notation Simplifies Calculations: Decimals are easier to add, subtract, multiply, or divide.
- Comparison and Estimation: Comparing fractions becomes straightforward when they are in decimal form.
- Practical Applications: From measuring ingredients in recipes to understanding financial statements, decimals are often the preferred format.
Understanding the Basics

Before we dive into the worksheet, it’s crucial to revisit some fundamental concepts:
- Denominator and Numerator: The denominator (the number below the line) indicates the number of equal parts the whole is divided into. The numerator (the number above the line) tells you how many of those parts are considered.
- Decimal Point: Represents a separation between the whole numbers and the parts.
The Fraction to Decimal Conversion Process

Let’s break down the conversion process:
- Divide the Numerator by the Denominator: This step directly gives us the decimal form. For example, for the fraction 1⁄4:
- Set up the division: 1 ÷ 4
- The result is 0.25, which is our decimal representation.
Using the Interactive Worksheet

To get the most out of your learning experience, we’ve prepared an interactive worksheet that guides you through the conversion process:
The worksheet includes:
- Various fractions to convert.
- Space for you to work out each problem.
- Immediate Feedback: Correct or incorrect answers are highlighted as you input your solution.
🔍 Note: For precise conversion in the worksheet, use the provided calculator tool to verify your manual calculations.
Common Challenges and Solutions

Here are some obstacles you might face along with solutions:
- Repeating Decimals: Some fractions lead to repeating decimals (e.g., 1⁄3 = 0.33333…). Use a bar over the repeating digits or round to a specified number of decimal places.
- Calculator Precision: Scientific calculators might display fractions differently due to limited decimal points. Understanding this helps you interpret results correctly.
| Fraction | Decimal | Calculator Notation |
|---|---|---|
| 1/3 | 0.3̅ | 0.3333... |
| 5/9 | 0.5̅ | 0.5556... |
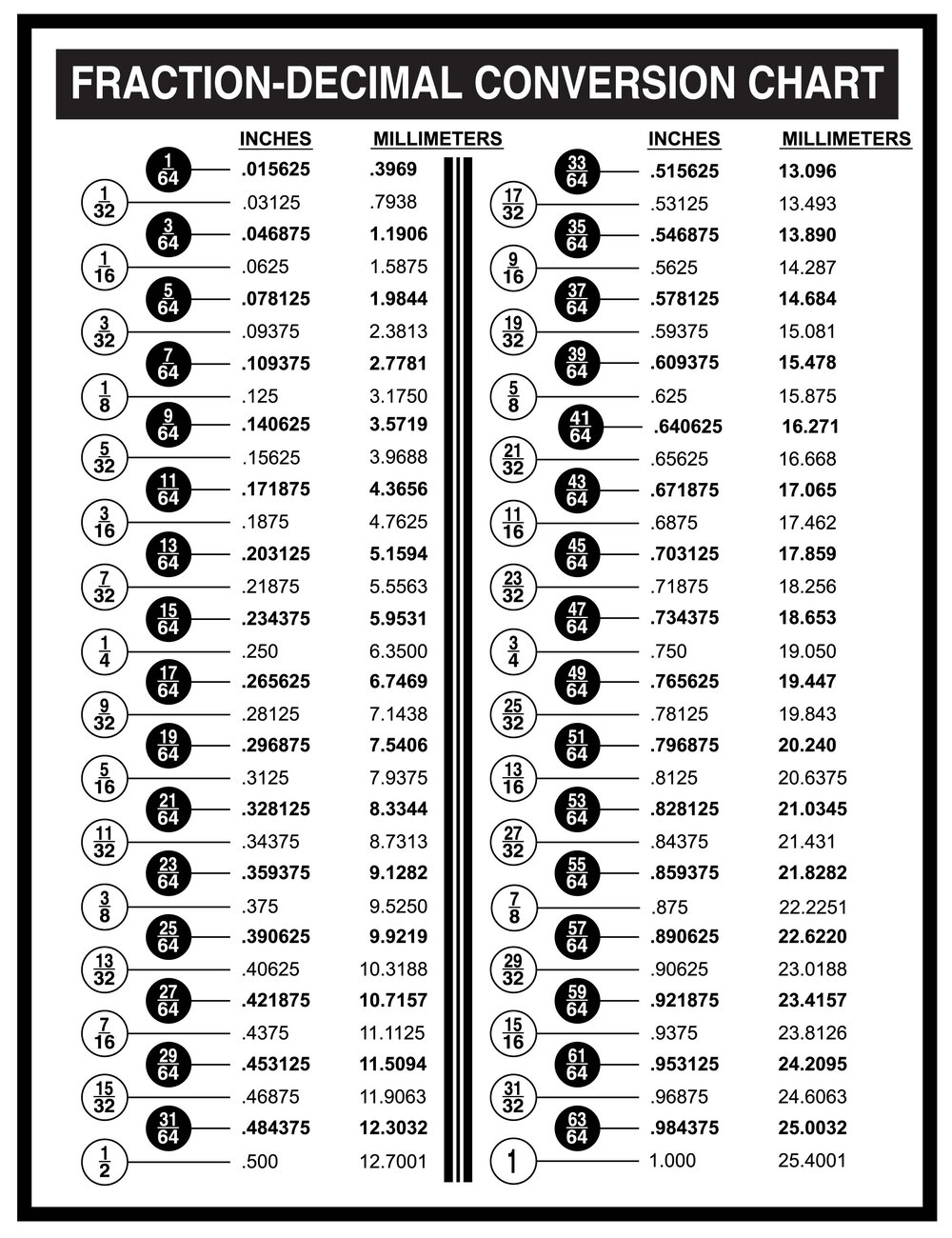
Mastering Decimal Conversion with Real-World Applications

Understanding the process of converting fractions to decimals is one thing; applying it in real-world situations is another:
- Banking and Finance: When dealing with interest rates, currency conversions, or investments, decimals make complex calculations simpler.
- Science: Experimental data often requires conversion for analysis.
- Cooking and Recipe Adjustments: Adjusting recipes involves precise measurements where decimals help in scaling quantities.
Mastering the Process

To solidify your understanding, continue practicing with the interactive worksheet:
- Challenge yourself with more complex fractions.
- Experiment with rounding to different decimal places.
📝 Note: Revisiting these concepts regularly can enhance your understanding and speed in converting fractions to decimals.
To summarize, converting fractions to decimals is more than a mathematical operation; it's a skill with numerous applications in our daily lives. By mastering this process, you can handle numerical challenges with ease, improve your problem-solving skills, and appreciate the elegance of math in simplifying complex situations. This guide has walked you through the essentials, from the basic theory to practical applications, ensuring that you not only understand the "how" but also the "why" behind fraction to decimal conversion.
Why do some fractions convert to repeating decimals?

+
Some fractions, when divided, result in a division that does not end, leading to repeating decimals. This happens due to the nature of division where certain numerators and denominators do not divide evenly, causing the decimal sequence to repeat indefinitely.
How do I represent a repeating decimal in writing?

+
Repeating decimals are often represented using a vinculum (overbar or underscore). For instance, 1⁄3 can be written as 0.3̅.
What’s the difference between a terminating and a non-terminating decimal?

+
A terminating decimal is one where the division of the numerator by the denominator results in a number that can be expressed without a repeating sequence. Non-terminating decimals, however, contain repeating digits or sequences after the decimal point.


