Master Piecewise Functions with Our Worksheet 2

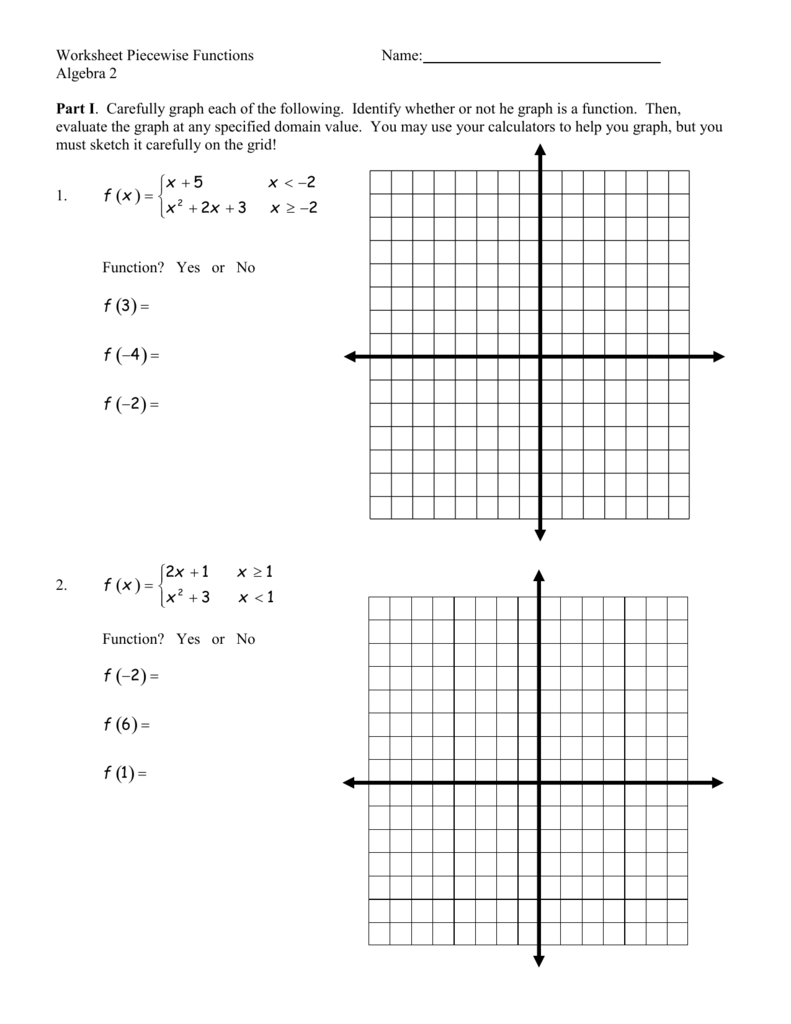
Understanding Piecewise Functions

Piecewise functions are mathematical constructs where a single function is defined by multiple sub-functions, each corresponding to a different interval of the function's domain. Think of them as a puzzle where different parts come together to form one coherent picture. These functions are pivotal in various fields such as economics, engineering, and computer science due to their ability to model different behaviors in different conditions.

Basic Definition

A piecewise function is a function which is defined by multiple sub-functions over specific intervals. The general structure looks like this:

f(x) = {
    f1(x) when x ∈ (a, b)
    f2(x) when x ∈ [c, d)
    ...
    fn(x) when x ∈ [m, n]
}

Each f_i(x) is a different piece or segment of the function, applied only within its specified interval.

Why are Piecewise Functions Important?

• Flexibility: They allow modeling of complex situations where different rules or behaviors apply under different conditions.
• Real-world Applications: From tax brackets to the behavior of physical systems under different environments, piecewise functions simplify complex phenomena.
• Ease of Analysis: By breaking a function into parts, we can analyze each segment individually which can lead to clearer insights.

Mastering Piecewise Functions with Our Worksheet

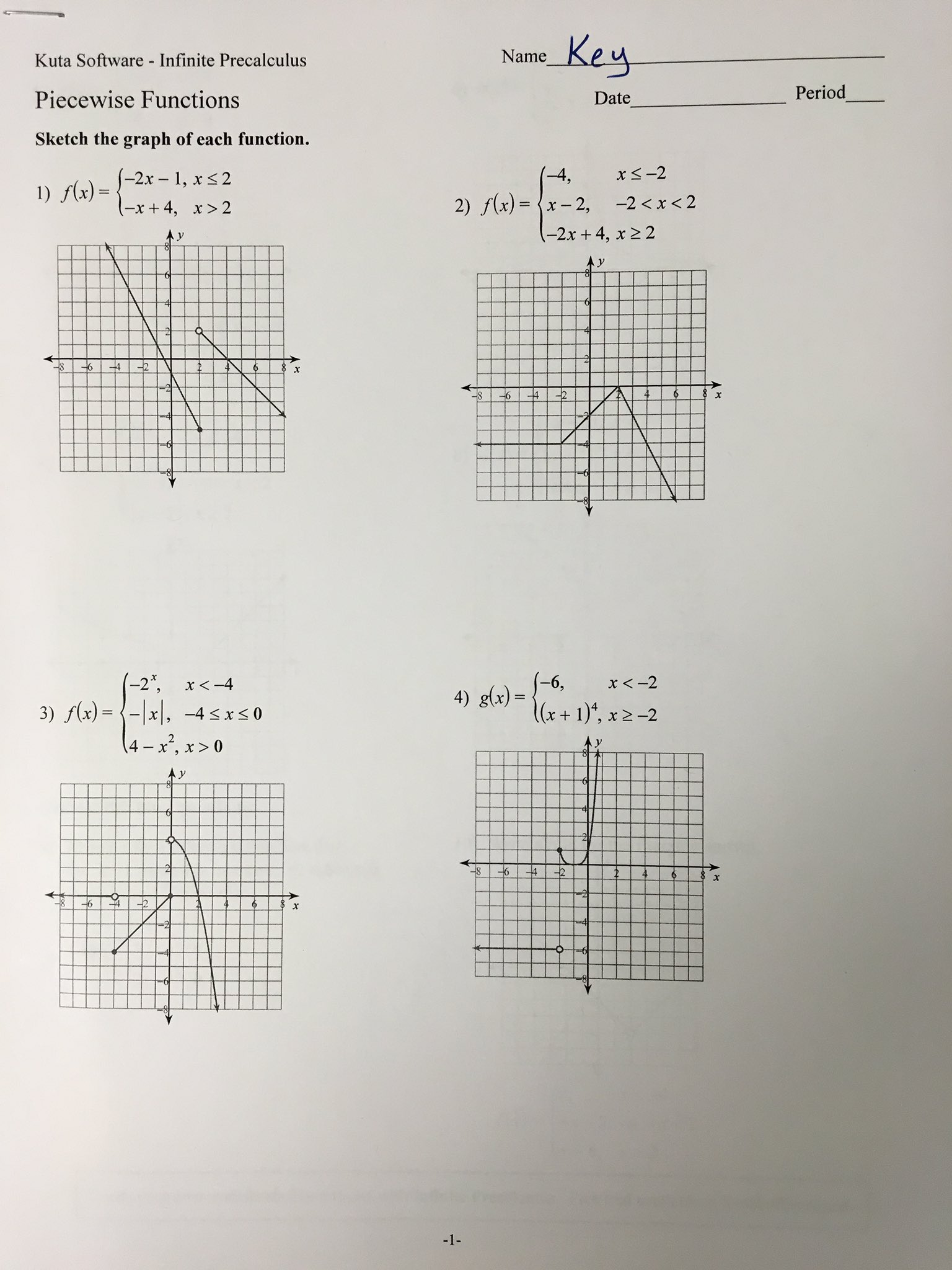
To truly grasp piecewise functions, practicing with worksheets is essential. Here’s how our worksheet can help you:

Exercise Variety

Our worksheet provides a broad range of exercises, from basic to advanced, ensuring that learners can:

• Understand the basic definition and evaluation of piecewise functions.
• Learn to plot these functions on a graph, understanding domain and range.
• Address real-world scenarios where piecewise functions are relevant.

Graphing Piecewise Functions

One of the most important aspects of mastering piecewise functions is visualizing them. Our worksheet includes exercises to:

• Plot simple piecewise functions, understanding discontinuities and domain intervals.
• Work with functions involving both continuous and discrete sections.
• Encounter exercises where you'll translate real-world scenarios into graphical representations.

Solving Problems with Piecewise Functions

Beyond graphing, applying piecewise functions to solve problems is crucial. Here's what you'll encounter in our worksheet:

• Evaluating function values at specific points.
• Understanding function behavior in different intervals.
• Translating mathematical problems into piecewise functions and vice versa.

📘 Note: Remember, when dealing with piecewise functions, always pay attention to where each piece is defined. This ensures accuracy when evaluating the function.

Additional Learning Resources

While our worksheet is an excellent starting point, supplementing your study with additional resources can be beneficial:

• Video Tutorials: Visual learners might find video guides on piecewise functions helpful.
• Interactive Apps: Use apps or online tools that allow you to play with different piecewise functions, observing how changes affect the graph and the function's behavior.
• Textbooks and References: Deep dive into theory with well-structured books that explain the intricacies of piecewise functions.

Final Thoughts

Mastering piecewise functions is not just about academic achievement; it's about acquiring a toolset for problem-solving in various real-world scenarios. Through our worksheet, you'll embark on a journey from understanding the basics to applying these functions in practical situations. Remember, the key is consistent practice and a willingness to approach problems from multiple perspectives. With time and effort, piecewise functions will become second nature, allowing you to model and solve complex problems with ease.

How do I know which piece of the piecewise function to use?

+

Each piece of the function is defined for specific intervals. To determine which piece to use, check the domain or interval in which your x-value falls. For instance, if f(x) has a piece f₁(x) defined for x < 0, and another piece f₂(x) for x ≥ 0, you would use f₁(x) if x is negative and f₂(x) if x is zero or positive.

Can piecewise functions have gaps or discontinuities?

+

Yes, piecewise functions can indeed have gaps or discontinuities, especially at the points where different pieces meet. These are known as jump discontinuities or removable discontinuities depending on how the functions behave near these points.

How do piecewise functions relate to real-world problems?

+

Piecewise functions are incredibly useful for modeling situations where different rules apply in different circumstances. For example, in taxation, income is taxed at different rates based on income brackets. Similarly, in engineering, a system might behave differently under varying conditions of temperature, pressure, or load.