Piecewise Function Worksheet Answers: Simplify Math With Us

Understanding piecewise functions can seem daunting at first, but with the right guidance, it becomes a manageable and even enjoyable part of mathematics. Piecewise functions, which are essentially multiple functions combined into one based on specified intervals, allow for a more dynamic description of different behaviors of a variable over its range. In this detailed blog post, we'll delve deep into the concept of piecewise functions, providing examples, explanations, and solutions to common problems students might encounter.
What Are Piecewise Functions?

A piecewise function is defined by several sub-functions which apply over different intervals. Here’s what you need to know:
- Each sub-function describes the behavior of the entire function within a specific interval.
- The intervals are clearly defined to avoid any confusion on which sub-function to apply.
- The function changes its behavior at what are called transition points.
To visualize this, imagine a function that behaves differently for values less than 0, from 0 to 1, and values greater than 1. Each of these intervals would have its own defining function.
Examples of Piecewise Functions

Let’s look at some basic and advanced examples to solidify your understanding:
Example 1: Basic Piecewise Function
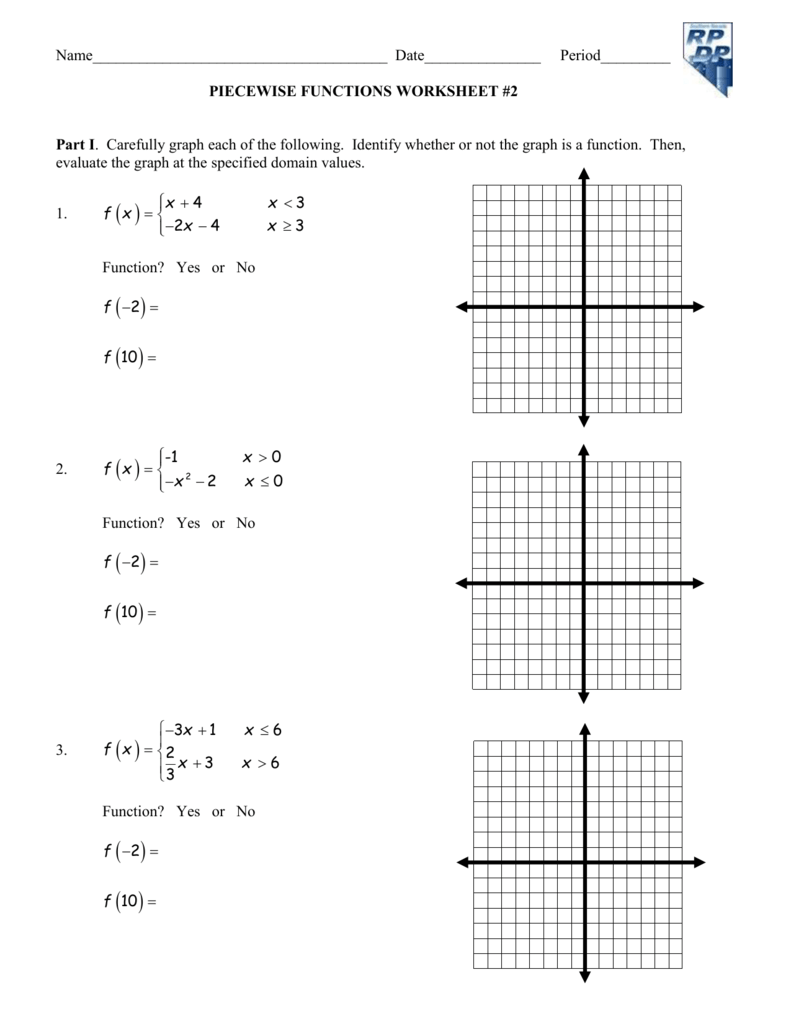
f(x) = {
-x - 2, x < 0
1, 0 ≤ x ≤ 1
x - 1, x > 1
}
In this example:
- For x less than 0, the function is f(x) = -x - 2.
- For x between 0 and 1 inclusive, the function is simply f(x) = 1.
- For x greater than 1, the function is f(x) = x - 1.
📌 Note: The sub-function that applies for x=0 and x=1 in this case would be f(x) = 1 because of the inclusive condition in the interval.
Example 2: Advanced Piecewise Function

g(x) = {
x^2 + 3, x ≤ -1
5 - x, -1 < x < 3
|x - 4|, x ≥ 3
}
Here, the function shows different behaviors:
- It’s a quadratic function for x ≤ -1.
- A linear function for -1 < x < 3.
- It switches to an absolute value function for x ≥ 3.
Simplifying Piecewise Function Problems

Here’s how to approach problems with piecewise functions:
- Identify Intervals: Clearly understand the boundaries of each sub-function.
- Apply the Correct Sub-function: Depending on the value of x, choose the appropriate sub-function to compute.
- Watch for Continuity: Ensure there are no discontinuities unless they are explicitly defined by the function.
Problem Solving Examples
Example 1:
Consider the function:
f(x) = {
x + 1, x < 0
2x, 0 ≤ x < 2
4, x ≥ 2
}
Find f(-1), f(1), and f(2).
- f(-1) = -1 + 1 = 0 (Using the first sub-function since x < 0).
- f(1) = 2 * 1 = 2 (Using the second sub-function since 0 ≤ x < 2).
- f(2) = 4 (Using the third sub-function since x ≥ 2).
Example 2:
Evaluate the piecewise function:
g(x) = {
x^3, x < -1
|x|, -1 ≤ x < 2
sqrt(x), x ≥ 2
}
Find g(-2), g(0), and g(4).
- g(-2) = (-2)^3 = -8 (Using the first sub-function since x < -1).
- g(0) = |0| = 0 (Using the second sub-function since -1 ≤ x < 2).
- g(4) = sqrt(4) = 2 (Using the third sub-function since x ≥ 2).
Important Notes on Working with Piecewise Functions

📌 Note: Always pay attention to the transition points. If a point lies on the boundary of two intervals, you must check both sub-functions to see which applies, especially if inclusivity is not clearly defined.
Having discussed the fundamentals and walked through examples, we can see that piecewise functions are tools that describe different behaviors of a function based on the input. By understanding how to interpret and apply these functions, students and enthusiasts can solve more complex problems in various mathematical contexts.
What is the purpose of piecewise functions?

+
Piecewise functions allow us to model situations where the behavior of a variable changes at specific points or intervals, offering a more accurate representation of real-world scenarios.
How do you solve problems with piecewise functions?

+
To solve problems with piecewise functions, identify the interval your input x falls into, and apply the sub-function corresponding to that interval.
Can piecewise functions be continuous?

+
Yes, piecewise functions can be continuous if the transition points match the values at the boundaries of their respective intervals or if they are designed to have no breaks.
Piecewise functions are indeed versatile and incredibly useful tools in mathematics. They enable us to represent complex scenarios where conditions change, allowing for nuanced problem-solving and graphical representations. Whether you’re preparing for a math exam or working on a real-world problem, understanding piecewise functions provides you with a powerful method to simplify and solve mathematical challenges. Remember, the key is to identify the correct interval and apply the corresponding rule. With practice, these functions will become second nature, opening up new dimensions in your understanding of mathematics.