Kepler's Law Worksheet: Solve with Ease

Understanding the motions of celestial bodies has been a cornerstone of astronomy since the dawn of civilization. In the 17th century, Johann Kepler, a German mathematician and astronomer, formulated three laws of planetary motion that revolutionized our understanding of the solar system. These laws, known as Kepler's laws, describe the orbits of planets around the sun with remarkable accuracy. Today, we'll delve into each of these laws, explore how they work, and provide a worksheet to help you solve problems using these principles.
Kepler’s First Law: The Law of Ellipses
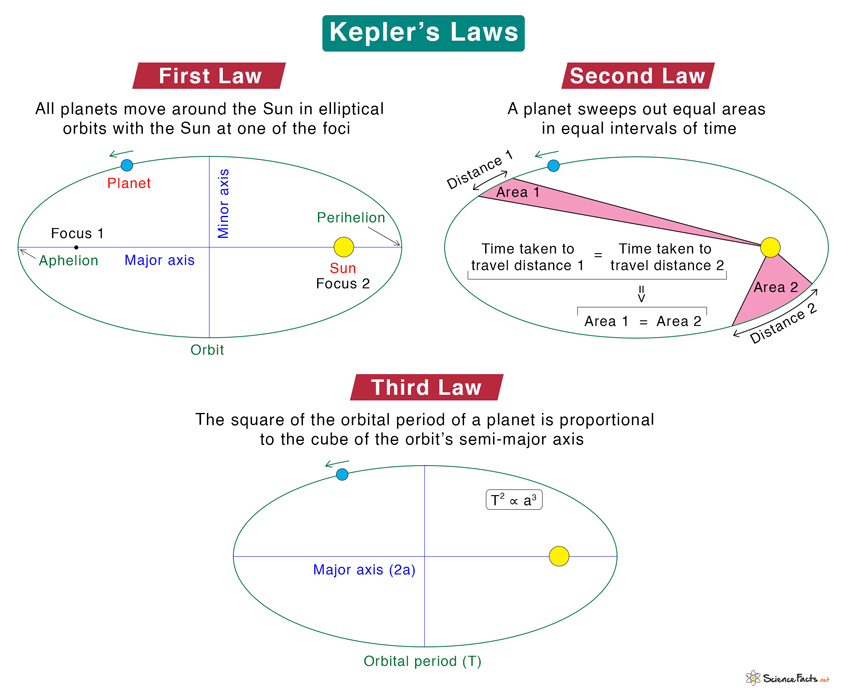
The first law, often referred to as the Law of Ellipses, states that the path of the planets around the sun is elliptical with the sun at one of the two foci. This was a significant departure from the previous belief that planetary orbits were circular.
- Planets orbit in ellipses, not circles.
- The sun is positioned at one focus of the ellipse, not at the center.
- The closer the focus is to the center, the more circular the ellipse.

Here's a simple worksheet exercise to solidify your understanding:
| Planet | Semi-Major Axis (a) | Perihelion Distance (r_p) | Calculate the Distance from the Sun to the Other Focus (c) |
|---|---|---|---|
| Earth | 1.0 AU | 0.983 AU | Calculate here |
| Mars | 1.524 AU | 1.381 AU | Calculate here |

🧠 Note: Remember, the semi-major axis (a) is the longest radius of the ellipse. To find the distance from the sun to the other focus (c), use the formula c = a - r_p, where r_p is the perihelion distance (the closest point to the sun).
Kepler’s Second Law: The Law of Equal Areas

Kepler’s second law, or the Law of Equal Areas, posits that a line joining a planet and the sun sweeps out equal areas in equal intervals of time. This means that a planet moves faster when it is closer to the sun (perihelion) and slower when it is farther away (aphelion).
- Planets move faster near perihelion and slower near aphelion.
- The speed of the planet is inversely proportional to its distance from the sun.

To practice this law, consider the following problem:
Given that Earth takes approximately 6 months to move from perihelion to aphelion, calculate how long it would take for Mars to cover the same area?
📚 Note: The time taken to sweep out equal areas is directly proportional to the planet's orbital period and inversely proportional to its velocity at that point. Use the relationship: Time = Orbital Period * (1/2).
Kepler’s Third Law: The Law of Harmonies

The third law, known as the Law of Harmonies, states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. Mathematically, this is represented as:
T^2 = k * a^3
Where:
- T is the orbital period in years.
- a is the semi-major axis in astronomical units (AU).
- k is Kepler’s constant, approximately 1.

Work through this worksheet exercise:
| Planet | Semi-Major Axis (a) | Orbital Period (T) | Calculate k (k = T^2/a^3) |
|---|---|---|---|
| Earth | 1.0 AU | 1.0 year | Calculate here |
| Mars | 1.524 AU | 1.881 years | Calculate here |
In summary, Kepler's laws provide us with a structured way to understand and predict the motion of celestial bodies around the sun. From the elliptical orbits to the relationship between distance and speed, and finally to the harmonic proportions of orbital periods, these laws have stood the test of time. They offer a practical framework for astronomers, astrophysicists, and enthusiasts alike to explore the cosmos. By working through the exercises, you not only gain a deeper appreciation for these laws but also enhance your problem-solving skills in the realm of celestial mechanics.
How were Kepler’s laws developed?

+
Kepler developed his laws by meticulously analyzing the astronomical observations made by Tycho Brahe, particularly data on the positions of Mars over several years. This empirical approach allowed him to find patterns that contradicted the then-prevailing Ptolemaic and Copernican systems, leading to his discovery of the elliptical orbits and other laws.
Are Kepler’s laws still relevant today?

+
Yes, Kepler’s laws remain essential for understanding basic planetary motion. While modern physics has introduced more complex models like general relativity for precise calculations, Kepler’s laws are fundamental and accurately describe motion within the solar system at speeds much less than the speed of light.
Can Kepler’s laws be applied to other systems?

+
Absolutely. Kepler’s laws apply to any two-body system where one body is significantly larger and affects the orbit of the smaller body, such as moons around planets, stars in binary systems, and even satellite orbits around Earth. However, adjustments must be made for three-body or more complex systems.