5 Steps to Master Perimeter Calculation of Triangles

The perimeter of a triangle is a foundational concept in geometry, providing the groundwork for understanding more complex shapes and calculations. Whether you're solving problems in a classroom setting or measuring the land for a garden project, knowing how to calculate a triangle's perimeter efficiently is crucial. In this guide, we will explore the five essential steps to mastering the calculation of the perimeter of any triangle, ensuring accuracy and ease in your measurements.
Understanding Perimeter: Basics

Before delving into complex calculations, it's beneficial to grasp what perimeter means:
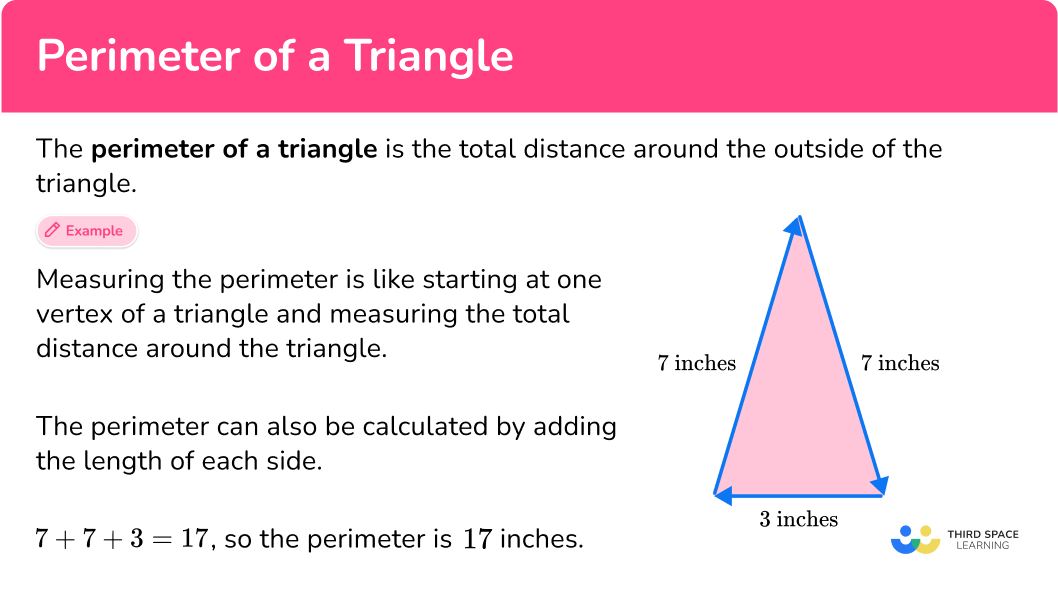
- Definition: The perimeter of a triangle is the total length of all its sides.
- Formula: Perimeter (P) = Side A + Side B + Side C
Note that for different types of triangles (equilateral, isosceles, scalene), while the formula remains the same, the values for the sides might change.
Step 1: Identifying the Triangle Type

Knowing the type of triangle you're dealing with can simplify your calculations:
- Equilateral Triangle: All sides are equal. Thus, P = 3 * any side length.
- Isosceles Triangle: Two sides are equal; calculate one unique side's length and add twice the other equal sides.
- Scalene Triangle: All sides are different; measure or calculate each side individually.
🔍 Note: The triangle identification is key because it affects how you measure or calculate side lengths.
Step 2: Measuring Sides Accurately

Accurate measurements are the bedrock of any perimeter calculation:
- Use a ruler, tape measure, or measuring wheel for physical triangles.
- For calculations, ensure you're using accurate unit measurements. Example: A triangle with sides 3 cm, 4 cm, and 5 cm.
Step 3: Apply the Perimeter Formula

With measurements in hand, apply the perimeter formula:
\[ P = A + B + C \]
- Equilateral Example: If all sides are 5 units, P = 5 + 5 + 5 = 15 units.
- Isosceles Example: With sides 4 units, 6 units, and 6 units, P = 4 + 6 + 6 = 16 units.
- Scalene Example: If sides are 3 units, 4 units, and 5 units, P = 3 + 4 + 5 = 12 units.
Step 4: Using Technology for Precision

To ensure accuracy, especially in complex or non-standard situations:
- Utilize calculators or apps that can compute perimeters instantly.
- Consider digital tools like CAD software for precise measurements in design projects.
🔍 Note: Technology provides a quick and error-free way to verify your manual calculations.
Step 5: Practical Applications

Understanding perimeter calculation goes beyond academic exercises:
- Garden Design: Calculate the amount of fencing needed.
- Construction: Measure the perimeter for material estimation.
- Art and Craft: Use perimeter to design triangular pieces in mosaic work or patchwork.
In summary, mastering the calculation of a triangle's perimeter involves understanding the basics, identifying triangle types, measuring accurately, applying the formula correctly, and leveraging technology. This foundational skill opens doors to various practical applications, making it an invaluable tool in your mathematical and real-world toolkit.
Why is it important to accurately calculate the perimeter of a triangle?

+
Accurate perimeter calculation is essential for real-world applications where space and material estimation are critical. Errors can lead to over-ordering materials or miscalculating space, potentially causing project delays or increased costs.
Can I calculate the perimeter of a triangle if I only know the base and height?

+
Unfortunately, no. The height alone does not provide information about the sides’ lengths, which are necessary for perimeter calculation. You’ll need at least two side lengths to proceed.
What if I measure the sides wrong, does it greatly affect the perimeter?
+
Yes, even a slight inaccuracy in measuring side lengths can lead to a significant difference in the perimeter. Ensuring precision in your measurements is key to accurate calculations.
How can digital tools enhance the process of calculating perimeter?

+
Digital tools like calculators, measuring apps, and CAD software automate the process, reducing human error, increasing speed, and providing instant feedback on calculations.