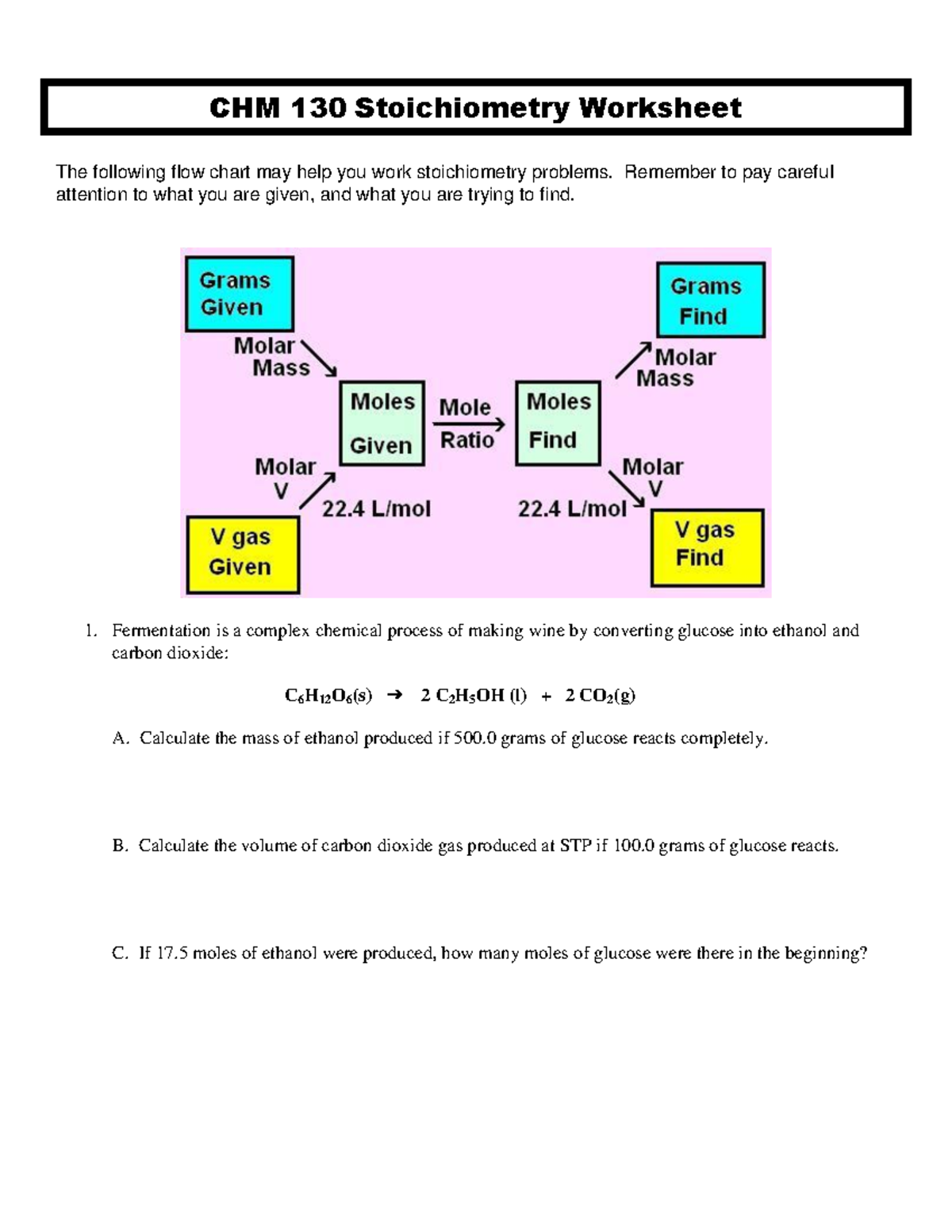
5 Essential Steps for Mastering Percent Composition in Chemistry

Understanding Percent Composition

Before diving into the complex world of chemical analysis, one must grasp the foundational concept of percent composition. This mathematical approach is vital for both academic pursuits and practical applications in various industries, from pharmaceuticals to metallurgy.

Percent composition, also known as weight percent, indicates how much mass a particular element contributes to a compound’s total mass. It is a measure of purity or concentration and is expressed as:
[ \text{Percent Composition} = \frac{\text{Mass of Element}}{\text{Total Mass of Compound}} \times 100 ]
This simple formula is at the heart of many chemistry-related calculations, informing everything from stoichiometric analysis to empirical formula determinations.
Step 1: Identify the Chemical Formula

The journey to mastering percent composition starts with accurately identifying the chemical formula of the substance in question. Here’s how to proceed:
Analyze the Compound: Determine the molecular or ionic formula of the compound. For example, consider sodium bicarbonate, NaHCO3.
List Elements: Identify all the elements within the formula, in this case, Sodium (Na), Hydrogen (H), Carbon ©, and Oxygen (O).
🔬 Note: Double-check the formula to ensure it is correct, as even minor mistakes can significantly alter your calculations.
Step 2: Calculate the Molar Mass of Each Element

Once the formula is known, the next step involves calculating the molar mass of each element present in the compound:
- Molar Mass: Use the periodic table to find the atomic mass (in amu) of each element and multiply by the number of atoms for that element in the compound.
| Element | Atomic Mass (amu) | Number of Atoms | Molar Mass (g/mol) |
|---|---|---|---|
| Na | 22.99 | 1 | 22.99 |
| H | 1.008 | 1 | 1.008 |
| C | 12.01 | 1 | 12.01 |
| O | 16.00 | 3 | 48.00 |

Step 3: Calculate the Molar Mass of the Compound

Add up the molar masses of all elements to determine the molar mass of the compound:
[ \text{Molar Mass of NaHCO}_3 = 22.99 + 1.008 + 12.01 + 48.00 = 84.01 \text{ g/mol} ]
Step 4: Determine the Mass Percent of Each Element

Now, apply the percent composition formula to calculate the mass percent of each element:
[ \text{Mass Percent of Na} = \frac{22.99 \text{ g/mol}}{84.01 \text{ g/mol}} \times 100 = 27.37\% ]
Repeat the calculation for each element:
- Hydrogen (H):
[ \text{Mass Percent of H} = \frac{1.008 \text{ g/mol}}{84.01 \text{ g/mol}} \times 100 = 1.20\% ]
- Carbon ©:
[ \text{Mass Percent of C} = \frac{12.01 \text{ g/mol}}{84.01 \text{ g/mol}} \times 100 = 14.31\% ]
- Oxygen (O):
[ \text{Mass Percent of O} = \frac{48.00 \text{ g/mol}}{84.01 \text{ g/mol}} \times 100 = 57.12\% ]
Step 5: Application and Verification

After calculating the percent composition, there are several practical applications:
Verification: The sum of the mass percentages should equal 100%. If your results don’t sum to 100%, recheck your calculations.
Chemical Identification: Compare the obtained percent composition to known values or use it for empirical formula determination.
Industrial Use: Apply this data to manage chemical purity, control reactions, and ensure product consistency.
⚗️ Note: Always verify your calculations using dimensional analysis or multiple references to ensure accuracy.
Understanding the steps and calculations involved in determining percent composition equips chemists to delve deeper into complex chemical analyses. This proficiency not only prepares students for academic excellence but also prepares professionals for the rigors of the chemical industry.
By keeping these steps in mind, you’re set to confidently approach any challenge involving percent composition. The journey towards mastering this fundamental concept is paved with practice, attention to detail, and a solid understanding of the principles of chemistry.
What is the difference between percent composition and empirical formula?

+
Percent composition tells us the mass fraction of each element in a compound, whereas the empirical formula represents the simplest whole number ratio of atoms of each element in the compound.
Why is percent composition important in chemistry?

+
It is essential for determining the purity of a substance, controlling reactions, ensuring product consistency, and for stoichiometric analysis, which allows chemists to predict how much of each substance is involved in chemical reactions.
Can I use percent composition to identify an unknown compound?

+
Yes, percent composition can help in identifying an unknown compound by comparing the calculated composition with known data, although it might not be sufficient on its own and often requires further analysis.
How does one verify the accuracy of percent composition calculations?

+
You can verify your calculations by ensuring the total percentage of all elements equals 100% or by using stoichiometric analysis to determine the compound’s formula and compare it with known values.