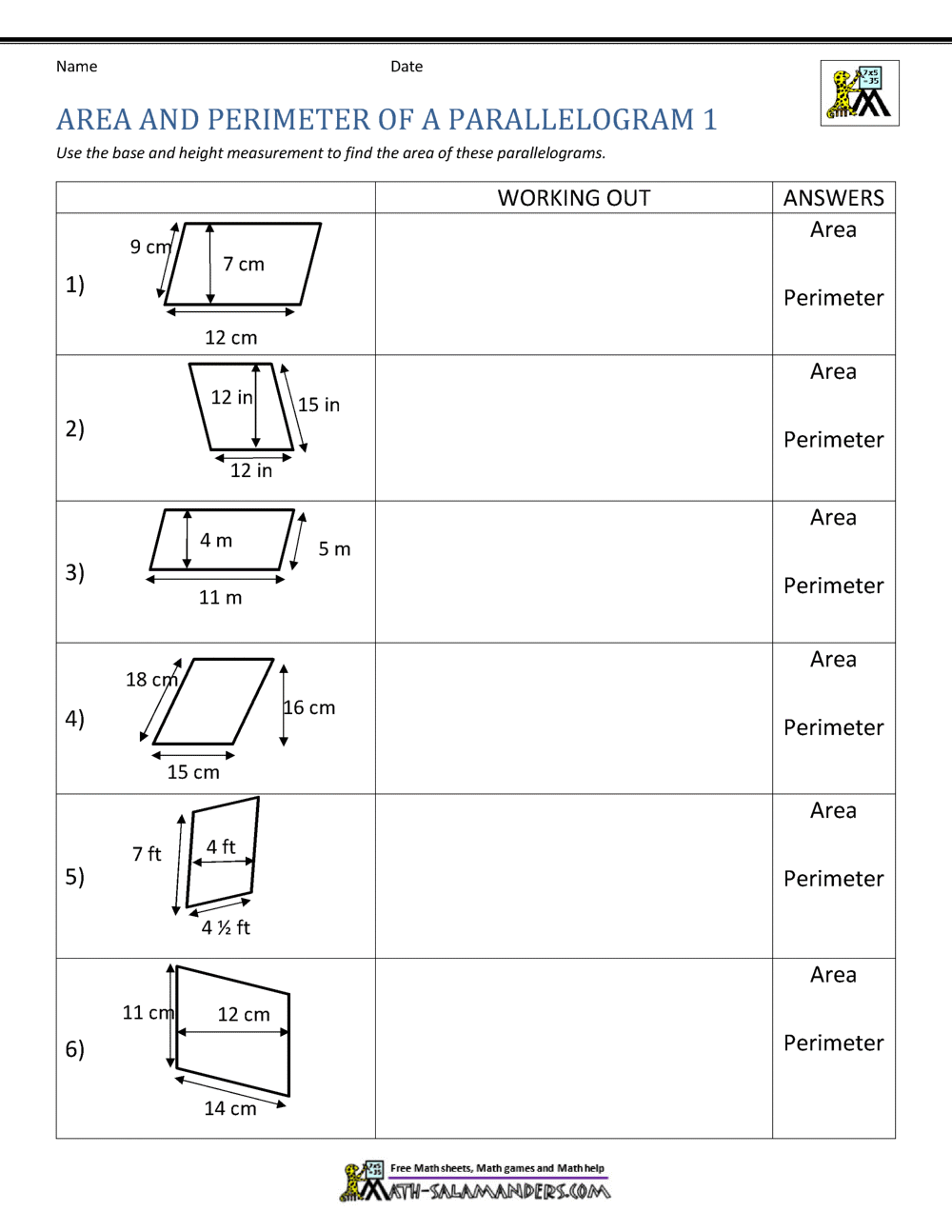
Parallelogram Practice Worksheet

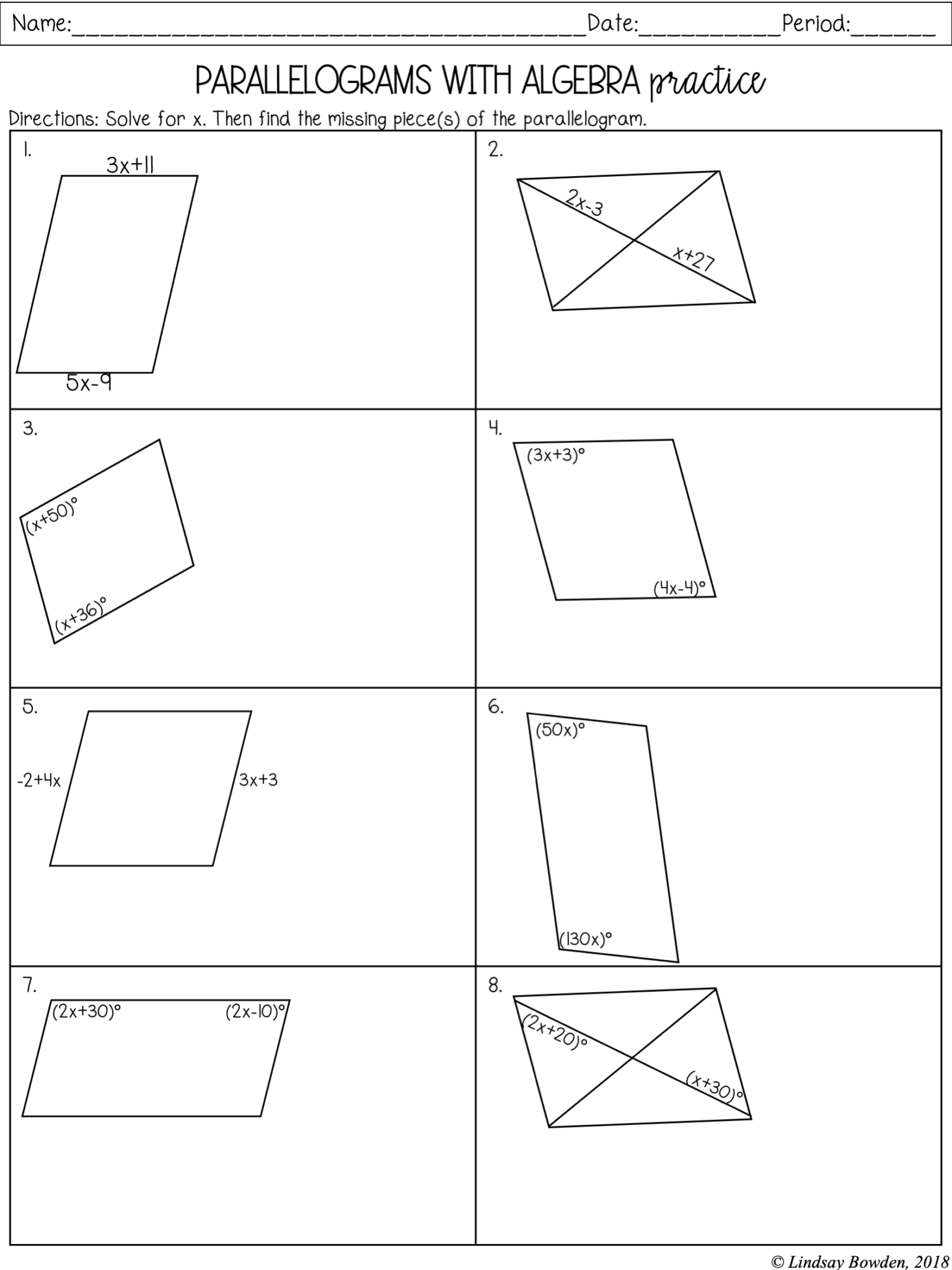
A parallelogram is a special type of quadrilateral where both pairs of opposite sides are parallel and equal in length. This geometric shape has several unique properties that make it an interesting subject for study and practice. In this worksheet, we'll explore these properties through various problems, encouraging hands-on learning and a deeper understanding of geometry. Let's dive in and sharpen our skills in dealing with parallelograms.

Properties of Parallelograms

Before we start with the practice problems, let's review some fundamental properties of parallelograms:

• Opposite sides are equal in length.
• Opposite angles are equal.
• The diagonals bisect each other.
• Adjacent angles are supplementary (sum to 180 degrees).
• The area can be calculated using base times height, or as the product of its diagonals and sine of the angle between them.

✅ Note: Understanding these properties will help you solve problems effectively.

Basic Calculations

Let's start with some basic calculations to familiarize ourselves with the shape:

1. Find the area of a parallelogram with base 10 units and height 5 units.
2. Given one diagonal of a parallelogram measures 14 units and the angle between the diagonals is 45 degrees, calculate its area.
3. One side of a parallelogram is 8 units, and the corresponding altitude is 4 units. What is its area?

🔍 Note: Remember that the area of a parallelogram can also be calculated using the sine formula with diagonals and angles.

Coordinate Geometry Problems

Here are some problems involving coordinates to further apply the properties:

1. Given vertices at (1,3), (5,3), (6,7), and (2,7), show that the quadrilateral formed is a parallelogram. Calculate its area.
2. Find the equation of the lines containing the diagonals of the parallelogram mentioned above.
3. If one side of a parallelogram is along the line 2x + y - 1 = 0 and its area is 36 sq units, find its height.

🧮 Note: Coordinate geometry involves working with straight lines and their equations, helping you understand the shape in a different context.

Trigonometry and Parallelograms

Let’s explore how trigonometry can be applied to parallelograms:

1. Find the length of one side of a parallelogram if its diagonals are 16 units and 30 units, and the angle between them is 60 degrees.
2. A parallelogram has sides of length 8 units and 6 units. If the acute angle between them is 30 degrees, calculate the area.

Proofs and Properties

Now, let’s delve into proving some of the properties:

1. Prove that in any parallelogram, the sum of the squares of the sides equals the sum of the squares of the diagonals.
2. Show that the area of a parallelogram can be expressed as half the product of its diagonals and the sine of the included angle.

📝 Note: Proofs help in solidifying your understanding of geometric shapes by demonstrating why properties hold true.

Parallelograms are not just fascinating shapes due to their properties but also because they connect various areas of mathematics. From basic calculations to coordinate geometry, trigonometry, and proofs, we've covered a range of techniques to better understand this geometric figure. The versatility of parallelograms in both real-world applications and theoretical studies makes them a vital part of geometric education. By practicing with different types of problems, one can gain insights into the elegance of mathematics and enhance problem-solving skills. Remember, the key to mastering any geometric shape is consistent practice and a solid grasp of its properties.

How can I remember all properties of a parallelogram?

+

One effective way to remember the properties of parallelograms is through mnemonics or by drawing connections to real-life objects. For example, think of a parallelogram as a book cover where opposite sides are the covers of the book (equal in length), and the angles are how the covers meet when closed (opposite angles equal). You can also use acronyms like “OPAL” (Opposite sides, Angles, and Lengths are equal, and diagonals bisect each other) to help recall the key attributes.

Can all quadrilaterals be classified as parallelograms?

+

No, not all quadrilaterals are parallelograms. A quadrilateral is classified as a parallelogram only if its opposite sides are both parallel and equal in length. Other quadrilaterals like trapezoids, kites, and irregular quadrilaterals do not always meet these criteria.

What is the significance of diagonals in a parallelogram?

+

Diagonals in a parallelogram play several crucial roles. They bisect each other, meaning each diagonal divides the other into two equal segments. This property is used in proofs and calculations for properties like the area or the relationship between sides and diagonals. Additionally, diagonals help in determining symmetry and can be used to calculate the area when combined with trigonometry.