5 Tips for Mastering Parallel and Perpendicular Lines

When studying geometry, one of the foundational concepts you'll encounter is the relationship between parallel and perpendicular lines. Understanding these lines is crucial not only for solving mathematical problems but also for applications in various fields like architecture, engineering, and design. Here are five tips to help you master these concepts effectively:
1. Understand the Definitions

Before you dive deeper, ensure you have a solid grasp of what these lines are:
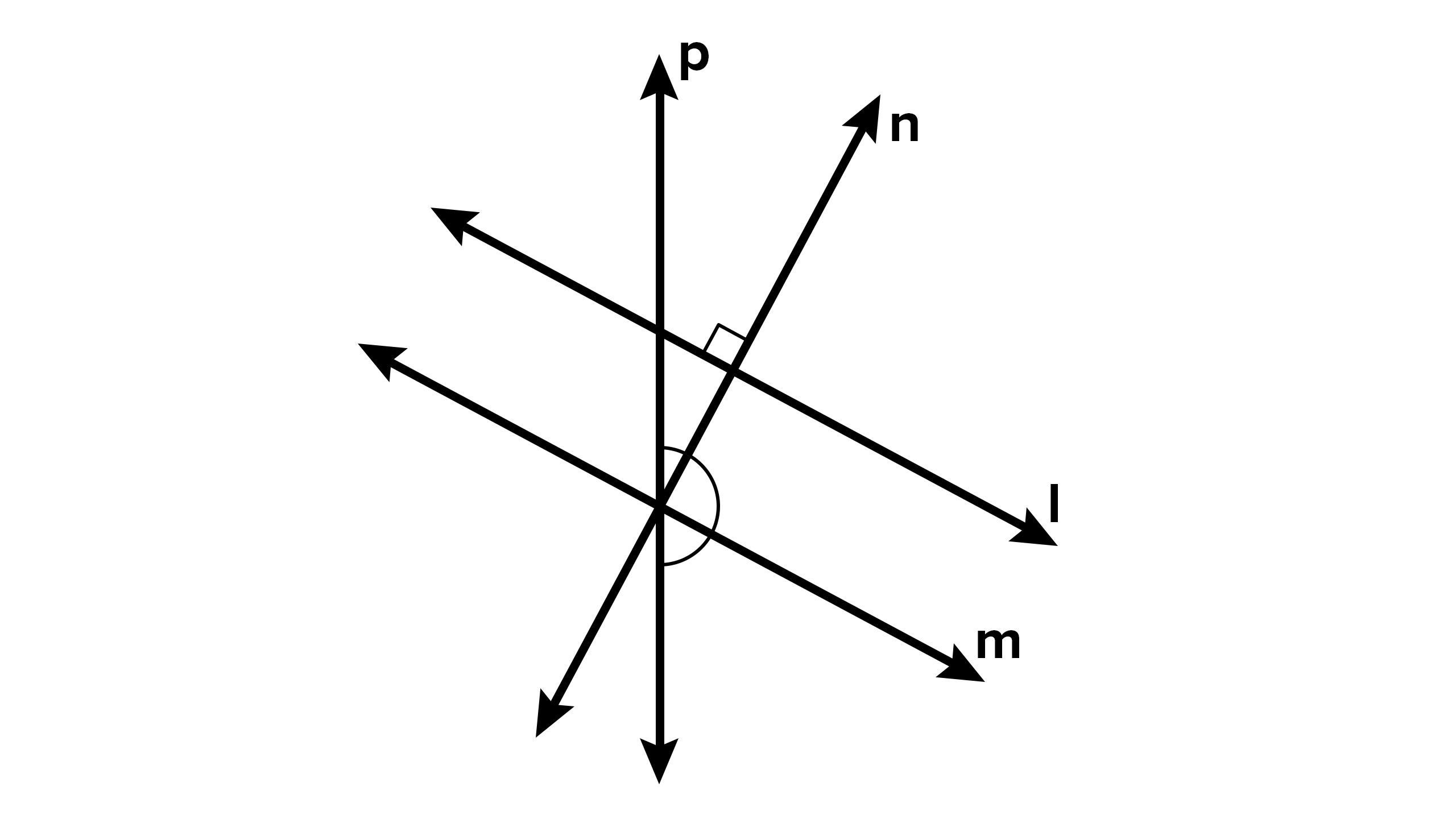
- Parallel Lines: Two lines are parallel if they are in the same plane and never intersect. They maintain an equal distance between each other throughout their lengths. In Euclidean geometry, this is often denoted as line A
 line B or simply A || B.
line B or simply A || B. - Perpendicular Lines: Two lines are perpendicular if they intersect at a right angle (90 degrees). This relationship is indicated by a box symbol (⊥) at the point of intersection.
2. Use Slope to Identify Line Relationships


In coordinate geometry:
- Parallel Lines: The slopes of parallel lines are equal. If line A has a slope of ’m’, then any line parallel to A will also have a slope of ’m’.
- Perpendicular Lines: The product of the slopes of two perpendicular lines is -1. If one line has a slope of ’m’, then a line perpendicular to it will have a slope of -1/m.
📝 Note: Remember that vertical lines have an undefined slope, which means they are perpendicular to horizontal lines (which have a slope of 0).
3. Apply Angle Properties


When two lines intersect:
- Parallel Lines: They form corresponding angles, alternate interior angles, and consecutive interior angles, which are either congruent or supplementary. Use these properties to prove lines are parallel.
- Perpendicular Lines: They form right angles at their intersection. Any angles that add up to 90° are complementary and can indicate perpendicularity.
4. Practice Drawing and Constructing Lines

Here is how you can improve your practical understanding:
| Step | Description |
|---|---|
| 1 | Use a straight edge to draw a line on your graph paper or drawing app. |
| 2 | Draw another line ensuring they do not intersect (parallel) or intersect at right angles (perpendicular). |
| 3 | Verify your constructions with a protractor or by measuring the slopes. |

5. Solve Problems Involving Parallel and Perpendicular Lines

To solidify your knowledge:
- Identify: Look for geometric figures or situations where these lines appear. Identify parallel and perpendicular relationships.
- Calculate: Use formulas to find unknown slopes or angles when given enough information.
- Prove: Construct proofs or verify given proofs about line relationships in geometric problems.
💡 Note: Regularly practicing problems from textbooks or online resources will greatly enhance your problem-solving skills.
Mastering parallel and perpendicular lines involves not just understanding their definitions and properties but also applying this knowledge to real-world scenarios and mathematical proofs. By immersing yourself in the mathematical language of these lines, practicing their construction, and solving related problems, you'll develop a strong foundation in geometry that can benefit many areas of study and practical application.
Why is it important to identify parallel and perpendicular lines?
+
Identifying these lines is crucial for solving geometric problems, designing structures, navigation, understanding optical systems, and many other practical applications where alignment, balance, and perpendicularity are important.
What are some real-life applications of parallel and perpendicular lines?

+
They are used in architecture for building stability and aesthetics, in engineering for precise construction, in road layouts for efficient traffic flow, in carpentry for framing, and in computer graphics for rendering 3D objects.
How can I remember the properties of perpendicular lines?

+
Remember that if you multiply the slopes of two perpendicular lines, you get -1. This relationship helps in quickly verifying perpendicularity when given equations or slopes of lines.
Can parallel lines be the same line?

+
In traditional Euclidean geometry, parallel lines are defined as distinct lines that never intersect. If they coincide, they are considered the same line, not parallel in the strict sense.
What’s the connection between angle measurement and line types?

+
Angles formed by intersecting lines directly relate to line type. Parallel lines form equal or supplementary angles when intersected by a transversal, while perpendicular lines form right angles at the intersection.



