Logarithm Worksheet Answers: Expanding and Condensing Mastery

Logarithms can often be daunting because they seem abstract and unrelated to day-to-day arithmetic. However, a fundamental understanding of logarithms is critical for students in advanced algebra, pre-calculus, and beyond. This blog post delves into two key operations with logarithms: expanding and condensing. We'll explore how these operations can enhance your mathematical toolkit, offering clarity and simplifying complex logarithmic expressions.

The Importance of Logarithms in Mathematics

Before we dive into the specifics, let's reflect on why logarithms matter:

• They Solve Exponential Equations: Logarithms are the inverse operations of exponentials, allowing for the direct solution of equations with variables as exponents.
• They Simplify Complex Calculations: Logarithms convert multiplication, division, exponentiation, and roots into simpler arithmetic operations.
• They're Essential in Various Fields: From engineering to economics, logarithms provide a model for phenomena that grow exponentially.

📝 Note: For this post, we'll focus solely on base 10 logarithms (common logarithms) unless otherwise stated.

Expanding Logarithms

Expanding logarithms involves breaking down a logarithmic expression into a sum, difference, or product of logarithms. This process can make complex expressions more manageable.

Properties for Expanding Logarithms

• Product Rule: log_a(mn) = log_a(m) + log_a(n)
• Quotient Rule: log_a(m/n) = log_a(m) - log_a(n)
• Power Rule: log_a(m^n) = n * log_a(m)

Step-by-Step Expansion Example

Let’s consider the logarithmic expression: log₁₀((x^2 * y^3) / z)

1. Apply Product Rule: log₁₀(x^2 * y^3 / z) = log₁₀(x^2) + log₁₀(y^3) - log₁₀(z)
2. Apply Power Rule: log₁₀(x^2) = 2 * log₁₀(x); log₁₀(y^3) = 3 * log₁₀(y)
3. Result: The final expansion is 2 * log₁₀(x) + 3 * log₁₀(y) - log₁₀(z)

💡 Note: Always ensure that the base of the logarithm is consistent throughout your expansions or condensations.

Condensing Logarithms

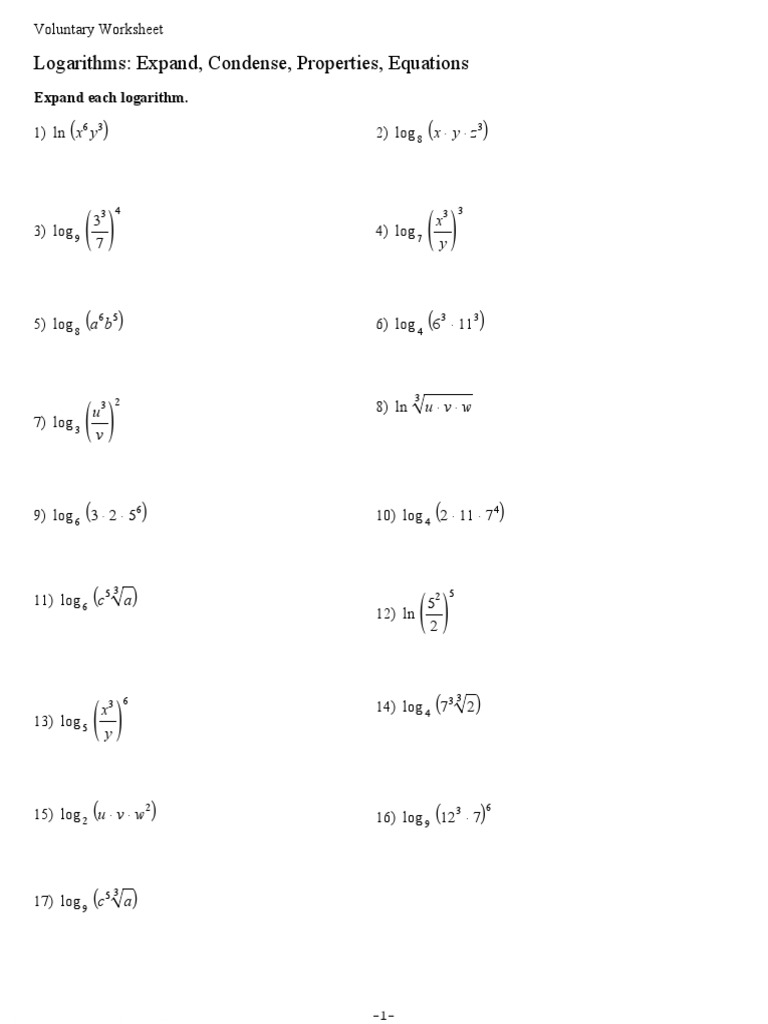
Condensing logarithms is the reverse process, where you combine individual logarithms into one. This can help simplify expressions or make them easier to solve.

Properties for Condensing Logarithms

• Product Rule: log_a(m) + log_a(n) = log_a(mn)
• Quotient Rule: log_a(m) - log_a(n) = log_a(m/n)
• Power Rule: n * log_a(m) = log_a(m^n)

Step-by-Step Condensing Example

Consider the expression: 4 * log₁₀(x) - log₁₀(y) + 2 * log₁₀(z)

1. Apply Power Rule: 4 * log₁₀(x) = log₁₀(x^4); 2 * log₁₀(z) = log₁₀(z^2)
2. Combine Using Product Rule: log₁₀(x^4 * z^2)
3. Apply Quotient Rule: log₁₀(x^4 * z^2) - log₁₀(y) = log₁₀((x^4 * z^2) / y)

🖊️ Note: Remember that when condensing, variables should be simplified into a single expression.

Applying Expansion and Condensing in Problem Solving

When tackling logarithmic problems, students can use expansion or condensation to simplify expressions before solving:

• Expanding: Useful when individual logarithmic terms need to be isolated or when logarithms must be split into sums or differences.
• Condensing: Often applied when you need to solve an equation involving multiple logarithms as one unified logarithmic expression.

Example Problem

Here’s an example of where both operations come into play:

Solve: log₁₀(x^3 * y^2 / z) + log₁₀(z)

1. Condense: log₁₀((x^3 * y^2 * z) / z) = log₁₀(x^3 * y^2)
2. Expand: log₁₀(x^3 * y^2) = 3 * log₁₀(x) + 2 * log₁₀(y)
3. Solve: If you’re given x and y values, you can now solve for the logarithmic expression.

What is the product rule in logarithms?

+

The product rule states that the logarithm of a product of two numbers is the sum of the logarithms of those numbers. Mathematically, log_a(mn) = log_a(m) + log_a(n).

Why do we need to expand and condense logarithms?

+

Expanding and condensing logarithms help simplify expressions for easier manipulation or solving, making complex logarithmic equations more manageable.

Can logarithms with different bases be directly expanded or condensed?

+

Logarithms with different bases cannot be directly combined or expanded using these rules. You would need to convert them to a common base before applying these properties.

In summary, understanding how to expand and condense logarithms is essential for students to master logarithmic functions. These techniques not only provide clarity in algebraic manipulation but also bridge the gap between the abstract concept of logarithms and their practical applications. By applying these rules, students can tackle complex problems with confidence, appreciating the elegance of logarithmic transformations in mathematics.