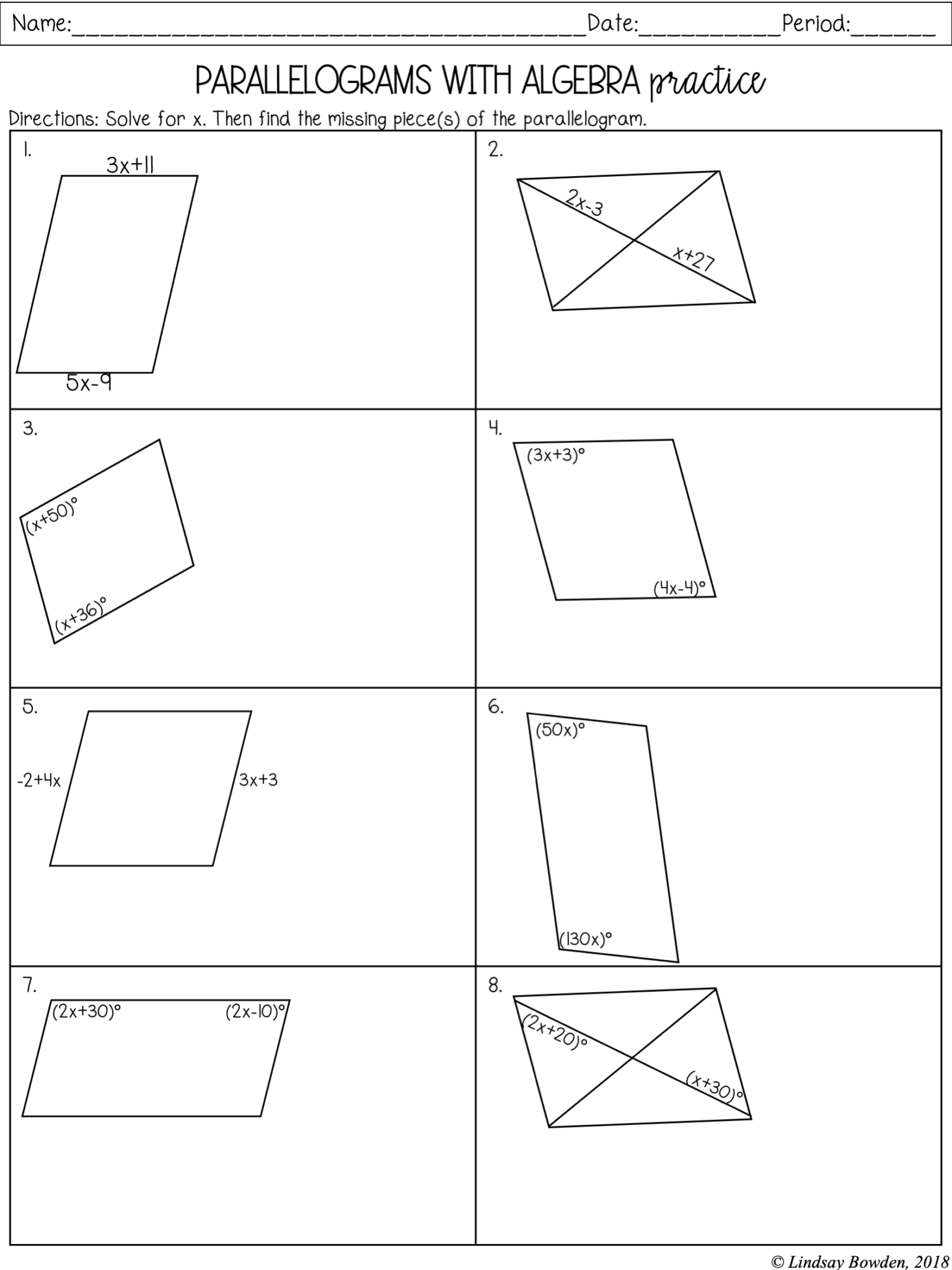
Master Parallel Lines Angles with Our Fun Worksheet

In the realm of geometry, understanding parallel lines angles is crucial for various mathematical concepts and applications. These angles can be both fascinating and challenging, especially for students starting their journey into geometry. Today, we're going to delve into a fun way to learn and master the angles formed by parallel lines using an engaging worksheet tailored for beginners and advanced learners alike.
What Are Parallel Lines?

Before we dive into the angles, it’s vital to have a clear understanding of parallel lines. Parallel lines are lines in the same plane that never intersect. They run infinitely close to each other but do not touch. Here are some key facts about parallel lines:
- They have the same slope.
- They are equidistant at every point.
- When cut by a transversal, they create several special angles.
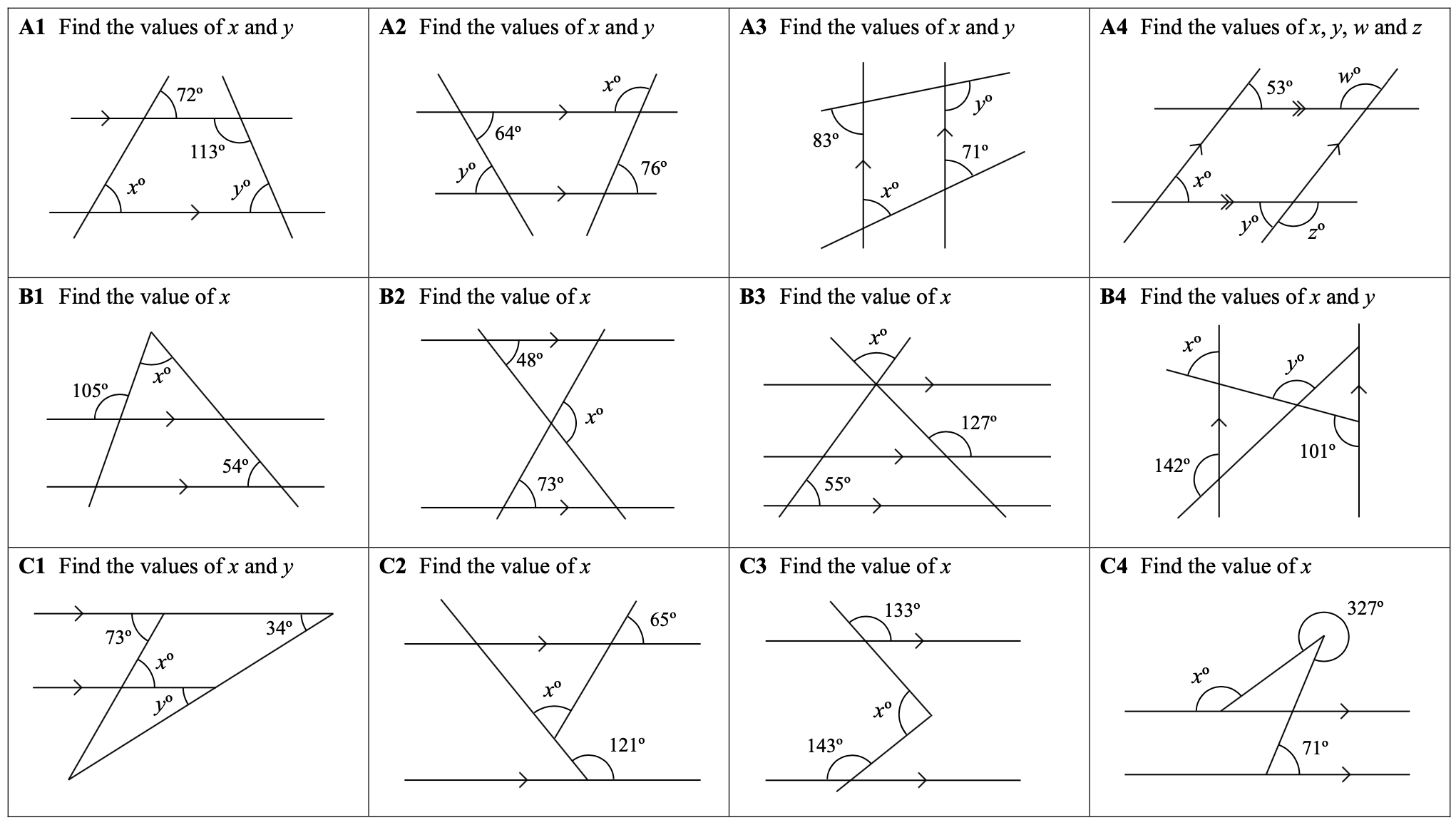
Types of Angles Formed by Parallel Lines and a Transversal

When a transversal intersects two parallel lines, it creates eight angles. Here’s a breakdown:
- Corresponding Angles: These angles are in the same position relative to the transversal. They are equal in measure.
- Alternate Interior Angles: Located between the parallel lines but on opposite sides of the transversal, these angles are also equal in measure.
- Alternate Exterior Angles: Outside the parallel lines and on opposite sides of the transversal, these angles are congruent as well.
- Consecutive Interior Angles: Also known as same-side interior angles, these are supplementary (sum to 180°).
- Vertical Angles: Directly opposite each other at the intersection points, these angles are always equal.
⚠️ Note: Remember that these properties only hold true if the lines are truly parallel.
Worksheet Activities for Mastering Parallel Lines Angles

Learning through doing is one of the most effective ways to internalize concepts in geometry. Here are some worksheet activities designed to help you master parallel lines angles:
Activity 1: Identify and Label Angles

In this activity, students are given diagrams where they must identify the types of angles created by a transversal:
- Label all corresponding angles.
- Identify and mark the alternate interior angles.
- Point out the consecutive interior angles.
- Find and label vertical angles.
| Angle Type | Example | Label |
|---|---|---|
| Corresponding | ∠1 and ∠5 | Blue |
| Alternate Interior | ∠2 and ∠8 | Green |
| Consecutive Interior | ∠4 and ∠6 | Red |
| Vertical | ∠3 and ∠7 | Purple |
📝 Note: Students should use different colors to highlight each angle type for better visualization.
Activity 2: Solve for Unknown Angles

This activity involves problem-solving where students apply angle properties:
- Given the measurement of one angle, find all other angles.
- Set up equations using the properties of angles (e.g., consecutive interior angles are supplementary).
- Solve for unknown variables in these equations.
Activity 3: Geometry Puzzles

Geometry puzzles can turn learning into an adventure:
- Design puzzles where students must arrange pieces to show all the angle relationships between parallel lines.
- Students can cut out angles and match them to their corresponding or supplementary partners.
By engaging in these activities, learners not only practice identifying angles but also understand their relationships and apply mathematical principles in a practical manner.
Conclusion

Understanding and mastering parallel lines angles is fundamental in geometry. Through the creative use of worksheets, students can approach this topic with enthusiasm and clarity. The activities outlined here aim to make learning interactive and enjoyable, ensuring that students grasp the concepts thoroughly. Remember, practice is key, and with these fun and structured exercises, the abstract can become concrete, making geometry accessible and enjoyable.
How do I know if lines are truly parallel?

+
Lines are parallel if they have the same slope or if a transversal forms corresponding angles that are equal, alternate interior angles that are equal, or consecutive interior angles that are supplementary.
What if the angles don’t match the expected properties?

+
If the angles do not match the expected properties, either the lines are not parallel or there might be an error in measurement or calculation. Check your work and ensure the lines are indeed parallel.
Why are the properties of angles important in geometry?

+
The properties of angles between parallel lines help in solving complex geometric problems, understanding spatial relationships, and in real-world applications like architecture, engineering, and design.