7 Essential Tips for Mastering Angle Pairs
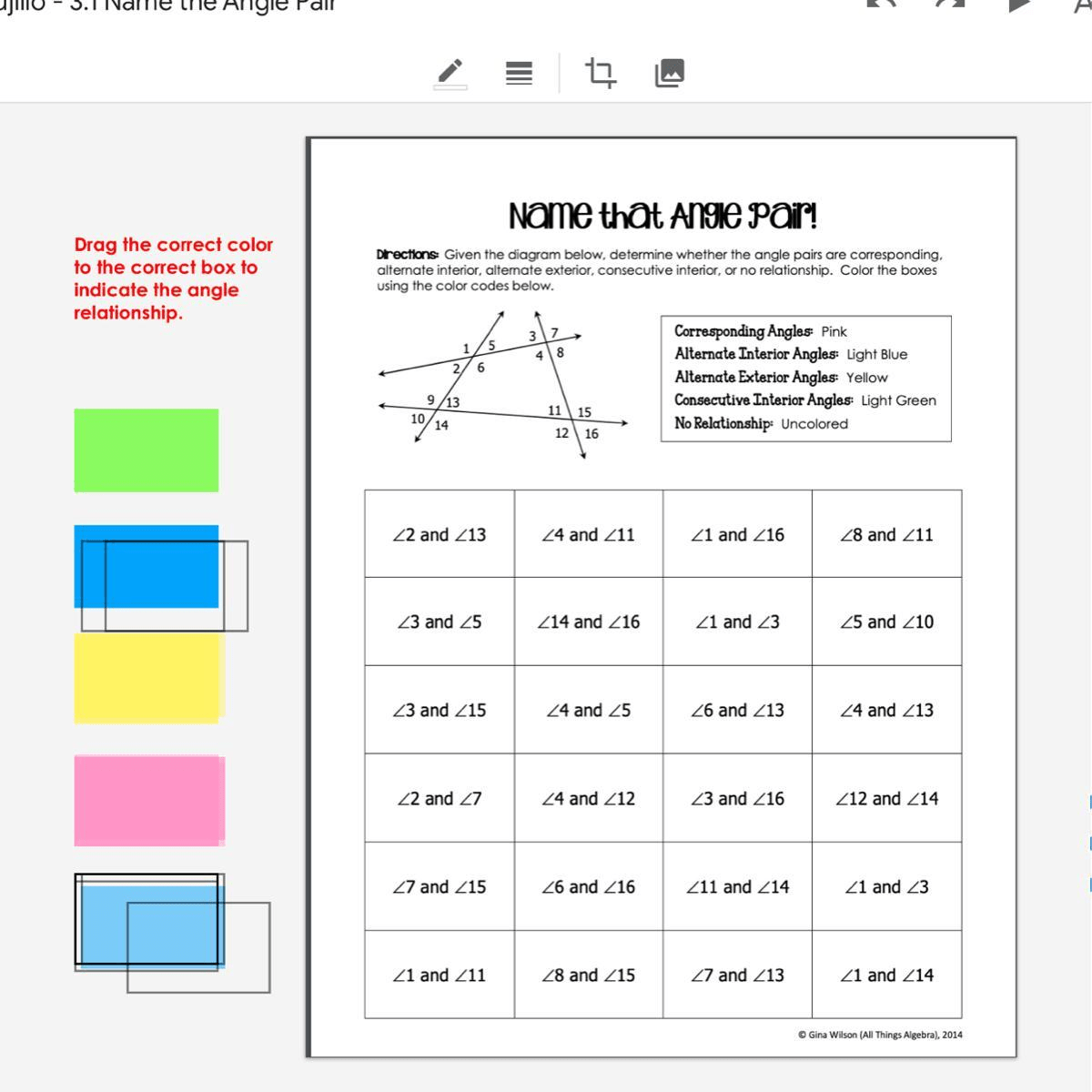
The exploration of geometry often begins with the understanding of angle pairs, which are fundamental for building a strong foundation in spatial reasoning and problem-solving. Angle pairs are groups of two angles that have certain relationships to one another based on their positioning. Mastering these concepts not only helps in solving geometric problems but also in understanding how angles interact in real-world scenarios. Here are seven essential tips to help you navigate through the intricate world of angle pairs effectively.
1. Understanding Basic Angle Terminology

Before diving deep into angle pairs, it’s crucial to grasp the basic terminology:
- Complementary Angles: Two angles whose measures add up to 90 degrees.
- Supplementary Angles: Angles that sum to 180 degrees.
- Adjacent Angles: Angles that share a common vertex, a common arm, but no interior points.
- Linear Pair: A pair of adjacent, supplementary angles.
⚠️ Note: These definitions are the cornerstone for understanding various angle pairs. Remembering them will help in recognizing and solving problems involving angles quickly.
2. Identify Angle Pairs by Their Positions

Visual recognition is key in geometry:
- Vertical Angles: Formed by two intersecting lines; they are opposite and congruent.
- Corresponding Angles: Located in the same position on two parallel lines cut by a transversal.
- Alternate Interior Angles: On opposite sides of the transversal but inside the parallel lines.
- Alternate Exterior Angles: On opposite sides of the transversal but outside the parallel lines.
- Consecutive (or Same-Side) Interior Angles: Between the parallel lines but on the same side of the transversal.
The positional relationship between angles helps in deducing their properties or measures without calculation.
3. Use Diagrams for Visualization


Diagrams are invaluable in geometry. They help in:
- Visualizing how angles are formed.
- Seeing which angles share special relationships.
- Quickly solving problems by recognizing these relationships.
4. Apply Theorems and Postulates

Geometry thrives on axioms, postulates, and theorems. Here are some you should be familiar with:
- Vertical Angles Theorem: Vertical angles are equal in measure.
- Corresponding Angles Postulate: If two parallel lines are cut by a transversal, then corresponding angles are congruent.
- Alternate Interior Angles Theorem: If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
Understanding these principles allows you to solve angle pair problems efficiently.
5. Utilize The Properties of Parallel Lines

When dealing with parallel lines, understanding the following properties can be extremely beneficial:
| Property | Description |
|---|---|
| Corresponding Angles | If lines are parallel, corresponding angles are congruent. |
| Alternate Angles | Alternate interior or exterior angles are congruent if lines are parallel. |
| Same-Side Interior Angles | If lines are parallel, same-side interior angles are supplementary. |

Knowing these properties can simplify the process of finding unknown angles or proving parallelism.
6. Practice Problem Solving

Geometry is best mastered through practice:
- Work through problems involving different types of angle pairs.
- Use both theoretical and practical exercises to reinforce your understanding.
Regular practice will help you recognize patterns and apply rules quickly.
7. Explore Advanced Concepts

Once you’re comfortable with basic angle pairs, delve into:
- Angle Bisectors: Lines or segments that divide angles into two equal parts.
- Exterior Angles: Angles formed by one side of a triangle and the extension of an adjacent side.
- Inscribed Angles: Angles whose vertices lie on a circle and whose sides are chords of that circle.
This will broaden your perspective and enhance your problem-solving skills in geometry.
As we wrap up this exploration into angle pairs, it's clear that mastering these concepts requires a blend of theoretical understanding and practical application. By internalizing the relationships between different angle pairs, using diagrams for visualization, and continually challenging yourself with new geometric problems, you'll find that what once seemed complex becomes straightforward. Remember, geometry isn't just about solving problems; it's about cultivating an understanding of space and shapes that applies to many fields of study and everyday life.
Why are angle pairs important in geometry?

+
Angle pairs are fundamental in geometry because they help in defining relationships between lines, points, and angles, simplifying problem-solving and proving geometric properties.
How can I remember all the types of angle pairs?

+
One effective method is to use visual aids like diagrams, associate mnemonic devices, and practice regularly. Understanding the concepts and their applications will also help with retention.
Can angle pairs help in real-world applications?

+
Absolutely, understanding angle pairs is crucial in fields like architecture, engineering, design, and navigation, where spatial relationships and angles are constantly applied.
What are the most common mistakes when dealing with angle pairs?

+
One common mistake is confusing types of angle pairs, especially between corresponding and alternate angles. Another error is misinterpreting supplementary and complementary angles or assuming parallel lines where none exist.



