Boost Math Skills: Multiplying Unit Fractions Worksheets

Multiplying unit fractions can be a fascinating mathematical journey, especially when you dive into the simplicity and elegance of these operations. Unit fractions, often overlooked in school curriculums, are fractions whose numerators are 1. This means they represent parts of a whole in the most fundamental way possible. This article will explore how to multiply unit fractions, providing insights, worksheets, and tips to enhance your math skills in this area.
Understanding Unit Fractions

A unit fraction is any fraction where the numerator is 1, and the denominator is a positive integer. Here are some examples:
- 1⁄2
- 1⁄3
- 1⁄4
When you multiply two unit fractions, you’re essentially looking at parts of parts, which makes the process both logical and easy to comprehend once you understand the underlying rules.
Multiplying Unit Fractions

To multiply two unit fractions, follow these steps:
- Multiply the numerators (Since both numerators are 1, this is always 1).
- Multiply the denominators to get the new denominator.
- The result is a new fraction with 1 as the numerator and the product of the denominators as the new denominator.
For instance, if you want to multiply 1⁄3 by 1⁄4:
- Numerator: 1 * 1 = 1
- Denominator: 3 * 4 = 12
- Result: 1⁄12
Worksheet for Practice

| Fraction 1 | Fraction 2 | Product |
|---|---|---|
| 1⁄2 | 1⁄3 | 1⁄6 |
| 1⁄4 | 1⁄5 | 1⁄20 |
| 1⁄3 | 1⁄7 | 1⁄21 |

📝 Note: Practice with different denominators to become comfortable with the multiplication of unit fractions.
Real-World Applications
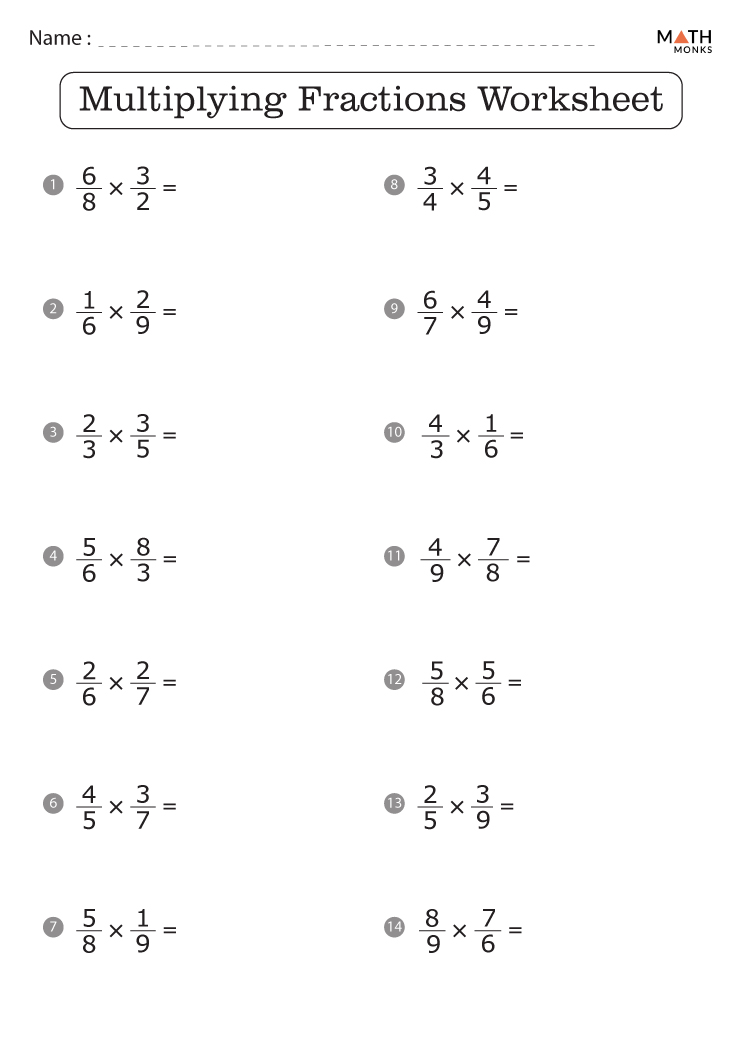
Multiplying unit fractions isn’t just a theoretical exercise. Here are some real-world scenarios where understanding this concept can be beneficial:
- Cooking: When recipes call for fractions of ingredients, sometimes you need to adjust for smaller servings or multiply for larger ones.
- Time Management: Dividing a time block into smaller parts, like studying or work sessions, can be conceptualized using unit fractions.
- Construction: When dealing with measurements or plans where precision is key, multiplying unit fractions can come into play.
Visual Aids for Learning
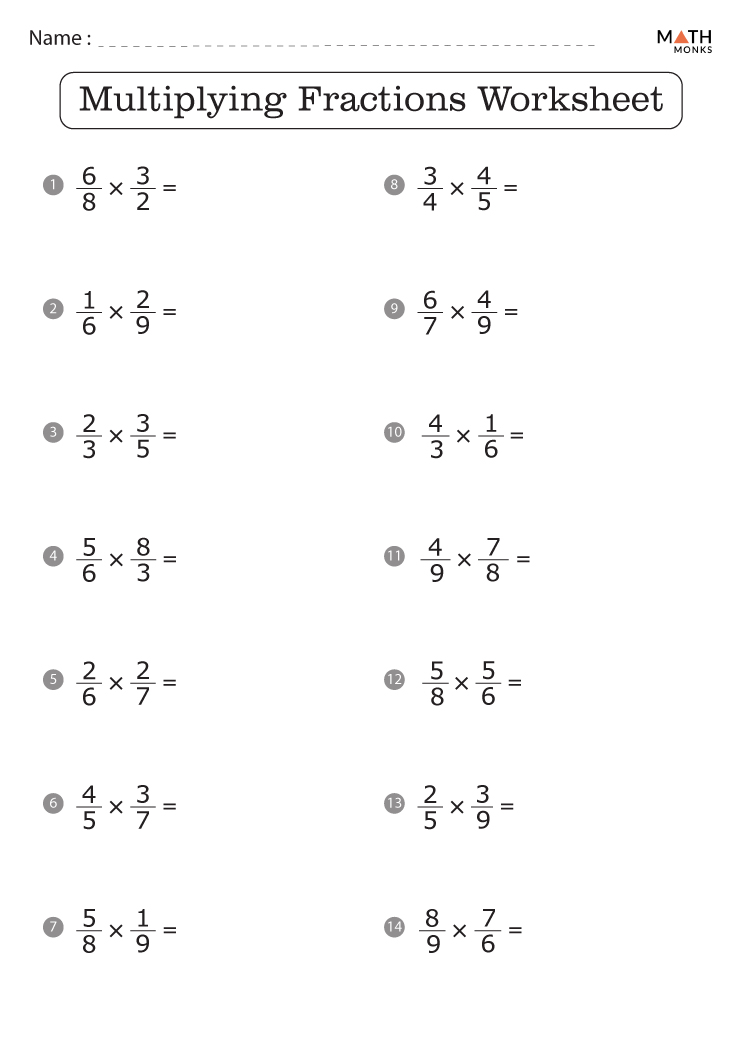
Visual aids can significantly help in understanding the process of multiplying unit fractions. Here’s how you can use visual aids:
- Diagrams: Draw rectangles or circles and divide them into parts according to the fractions being multiplied.
- Number Lines: Represent unit fractions on number lines and show how multiplication affects their placement.
Such visual representations can make abstract concepts more tangible and easier to grasp.
Enhancing Fluency with Repeated Practice

The key to mastering multiplication of unit fractions is repeated practice. Here are some tips:
- Practice with a variety of fractions, including less common denominators like 9 or 15.
- Use online tools or apps designed for fraction practice to gain speed and accuracy.
- Set up timed challenges to test your speed and precision in multiplying unit fractions.
To wrap up our journey through the world of multiplying unit fractions, it's clear that this concept, while simple, opens up numerous avenues for deeper mathematical understanding and practical application. By engaging with unit fractions, you not only sharpen your arithmetic skills but also develop a greater appreciation for the mathematical structure underpinning our daily lives. Whether in cooking, managing time, or even planning a garden, the principles you've learned here will serve you well. Keep practicing, exploring, and you'll find unit fractions are just the beginning of a broader numerical adventure.
Why are unit fractions important in mathematics?

+
Unit fractions serve as the building blocks of more complex fractions and are crucial for understanding division and fractional division in mathematics.
Can you multiply a unit fraction by a mixed number?

+
Yes, you can multiply a unit fraction by a mixed number, but first, you must convert the mixed number into an improper fraction before proceeding with multiplication.
How can I remember how to multiply unit fractions?

+
Remember that the numerator is always 1, so you only multiply the denominators to find the new denominator. The product will always be a unit fraction.



