5 Ways to Multiply Fractions and Mixed Numbers

The ability to multiply fractions and mixed numbers is essential in mathematics, especially when dealing with real-life applications such as baking, construction, or financial planning. Multiplying these numbers might seem intimidating at first, but with the right approach, it can become straightforward. In this post, we will explore five different methods to multiply fractions and mixed numbers, ensuring that you can tackle any related problem with confidence.
Method 1: Basic Multiplication of Fractions

The most common method to multiply fractions is to multiply the numerators together and the denominators together.
- Take the numerators of both fractions and multiply them.
- Multiply the denominators of both fractions.
- The resulting fraction might be reducible to a simpler form.
Example: Multiply 1⁄2 by 3⁄4.
- Numerators: 1 * 3 = 3
- Denominators: 2 * 4 = 8
- The result is 3⁄8.
🔍 Note: Always check if you can simplify the fraction before or after multiplication.
Method 2: Multiplying Mixed Numbers

Mixed numbers are fractions composed of a whole number and a proper fraction. Here's how to multiply them:
- Convert mixed numbers to improper fractions.
- Multiply the improper fractions using the basic method above.
- If necessary, convert the result back to a mixed number.
Example: Multiply 2 1⁄2 by 1 3⁄4.
- Convert 2 1⁄2 to an improper fraction: 5⁄2
- Convert 1 3⁄4 to an improper fraction: 7⁄4
- Multiply: (5⁄2) * (7⁄4) = 35⁄8
- Convert 35⁄8 back to a mixed number: 4 3⁄8
Method 3: Using Cross Cancellation

Cross cancellation can simplify the multiplication of fractions or mixed numbers by reducing numbers before multiplying.
- Align the fractions vertically to see both numerators and denominators.
- If possible, cancel out common factors in the numerator and denominator diagonally or vertically.
- Multiply the reduced numerators and denominators.
Example: Cross cancel 4⁄5 * 2⁄10.
- Cancel 5 in the denominator of the first fraction with the 10 in the denominator of the second fraction (since 5 is a factor of 10).
- Then, multiply 4⁄1 by 2⁄2 which simplifies to 8⁄2 = 4.
Method 4: Area Models for Multiplication

An area model can visually represent the multiplication of fractions or mixed numbers.
- Draw a rectangle and split it into sections that represent the fractions being multiplied.
- Shade in the appropriate parts to represent the multiplication.
- The total area shaded will represent the product of the fractions.
Example: Using an area model for 1⁄2 * 3⁄4.
- Draw a rectangle and divide it into 4 parts horizontally and 2 parts vertically.
- Shade 3⁄4 of the rectangle horizontally and 1⁄2 vertically, highlighting 3⁄8 of the total area.
Method 5: Using the Distributive Property

The distributive property can help multiply mixed numbers by breaking them down into simpler parts.
- Break the mixed number into a whole part and a fractional part.
- Multiply each part by the other number separately.
- Combine the products to get the final result.
Example: Multiply 3 1⁄2 by 2.
- 3 * 2 = 6
- 1⁄2 * 2 = 1⁄1 = 1
- Combine results: 6 + 1 = 7
🎨 Note: Visual methods like area models can be particularly useful when teaching or understanding multiplication of fractions for the first time.
In summary, multiplying fractions and mixed numbers can be approached in various ways, each with its benefits. From basic multiplication to employing the distributive property or visual techniques like area models, these methods offer flexibility in solving mathematical problems. Understanding these techniques allows you to approach complex fraction multiplication with ease, ensuring you have the tools necessary to handle any related challenge in mathematics or real-life applications.
When should I simplify a fraction during multiplication?
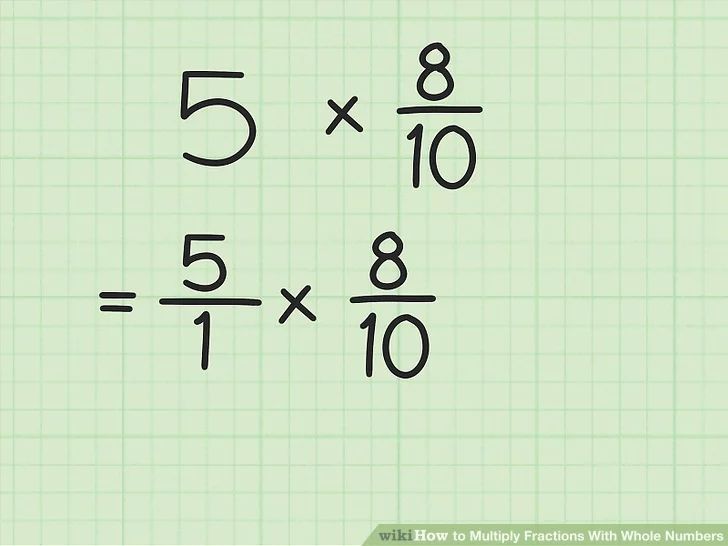
+
Simplify the fraction whenever you can, either before or after multiplication, to make the arithmetic easier.
Can I use these methods for other operations like division?

+
Yes, but division requires an extra step, converting the division into multiplication by the reciprocal of the divisor.
What are the advantages of using an area model?

+
Area models help in understanding the multiplication of fractions visually, making it easier to grasp the concept especially for visual learners.
How do you convert a mixed number to an improper fraction?

+
Multiply the whole number by the denominator of the fraction, add the numerator, and place this sum over the original denominator.



