Multiplying Binomials and Trinomials: Easy Worksheet Guide

Mastering the art of multiplying polynomials is a crucial skill in algebra, serving as the foundation for more advanced mathematical concepts. This guide aims to provide students with an easy-to-follow worksheet for multiplying binomials and trinomials, ensuring they grasp this essential algebra topic with confidence.
Understanding Polynomial Multiplication

Polynomial multiplication involves multiplying two or more polynomials together. Here are some key points to understand:
- Each term in the first polynomial is multiplied by each term in the second polynomial.
- The terms that result from these multiplications are then added together.
- Ensure to follow the distributive property to get the correct terms.
📘 Note: Polynomial multiplication is commutative; the order of multiplication does not change the result.
How to Multiply Binomials

Binomials are expressions with two terms, like ( (a + b) ) or ( (x - y) ). Multiplying them can be simplified using the FOIL method:
- First - Multiply the first terms in each binomial.
- Outer - Multiply the outer terms.
- Inner - Multiply the inner terms.
- Last - Multiply the last terms in each binomial.
Here’s an example:
(x + 3)(x - 2) = (x * x) + (x * -2) + (3 * x) + (3 * -2) = x2 - 2x + 3x - 6 = x2 + x - 6
✏️ Note: The FOIL method is specifically for multiplying two binomials.
Multiplying Trinomials

Trinomials contain three terms, and their multiplication involves:
- Distributing each term in one trinomial to all terms in the other trinomial.
- Adding like terms afterwards to simplify the expression.
Example:
(x2 + x - 1)(x + 3) = (x2 * x) + (x2 * 3) + (x * x) + (x * 3) + (-1 * x) + (-1 * 3) = x3 + 3x2 + x2 + 3x - x - 3 = x3 + 4x2 + 2x - 3
Worksheet Guide

| Problem | How to Solve |
|---|---|
| (x + 2)(x - 3) | Apply FOIL method |
| (x - y)(x + y) | Multiply and combine like terms |
| (a + b + c)(d - e) | Distribute terms |
| (2x + 1)(x^2 - 3x + 4) | Multiply each term in the trinomial by each term in the binomial |
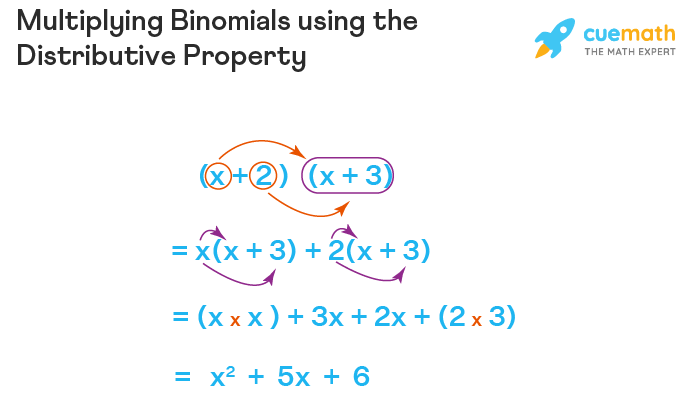
Practice Exercises

To enhance your understanding, here are some practice exercises:
- (x + 5)(x - 5)
- (2m - n)(2m + n)
- (y^2 + 3y + 1)(y - 1)
🏫 Note: Practicing these exercises regularly will reinforce your algebraic skills.
Understanding how to multiply polynomials, specifically binomials and trinomials, lays a strong foundation for future studies in mathematics. Whether you're preparing for a test or just trying to keep up with classwork, mastering these concepts will greatly improve your algebraic proficiency. With practice, what once seemed daunting will become a straightforward process, opening up further avenues of learning in mathematics and beyond.
Why is it important to multiply polynomials in algebra?

+
Multiplying polynomials helps in solving equations, simplifying expressions, and understanding the relationship between functions and their derivatives or integrals, which are essential in calculus.
Can I use the FOIL method for polynomials other than binomials?

+
While the FOIL method is specifically designed for binomials, you can use it as part of the distribution process when multiplying polynomials with more terms, but it requires careful handling of more terms.
What’s the difference between combining like terms and distributing in polynomial multiplication?

+
Combining like terms means adding or subtracting terms with the same variable to simplify expressions. Distributing involves multiplying each term in one polynomial by each term in another polynomial before combining like terms.