5 Simple Ways to Multiply Negative Numbers Easily
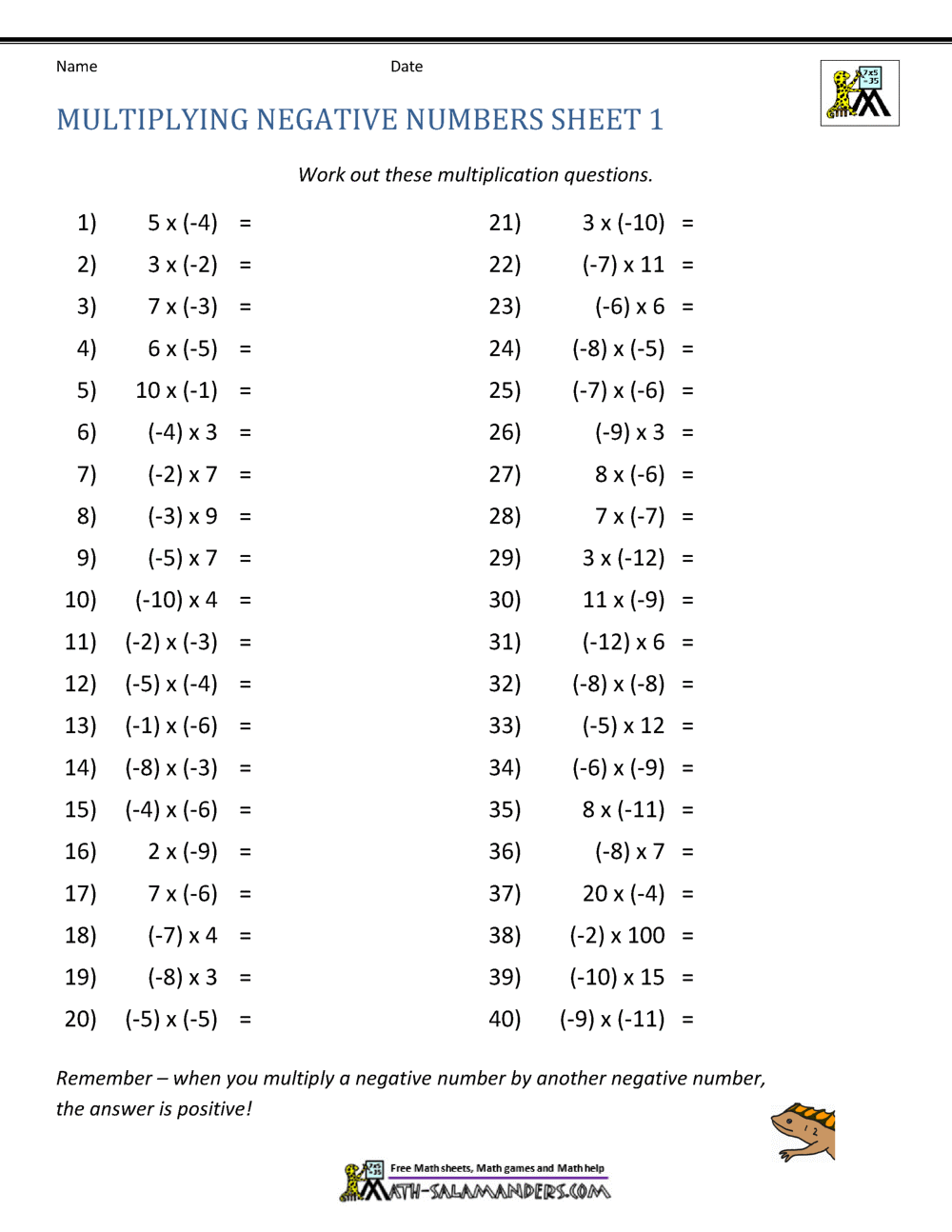
Navigating the world of mathematics, especially when it comes to operations with negative numbers, can sometimes be a daunting task for many students and even adults. However, multiplying negative numbers doesn't have to be as complicated as it seems. Here are five straightforward methods to make this operation much easier and intuitive.
Understanding the Basics

Before diving into the methods, it’s vital to grasp the fundamental rules of multiplying integers:
- Positive * Positive = Positive
- Negative * Negative = Positive
- Positive * Negative = Negative
- Negative * Positive = Negative
These rules are the cornerstone of multiplying negative numbers.
1. Visual Multiplication Table

Visual learning can simplify complex concepts. Create a multiplication table:
| + | - | |
|---|---|---|
| + | + | - |
| - | - | + |

Using this table, you can easily see that:
- Multiplying two positive numbers or two negative numbers gives a positive result.
- Multiplying a positive by a negative or vice versa results in a negative answer.
📌 Note: Use this method when you need a quick reference to understand the sign of the result.
2. The Sign Rule

This rule is straightforward:
- If the number of negative signs in the multiplication is even, the result is positive.
- If the number is odd, the result is negative.
For example, (-5) * (-3) * (-2) contains three negative signs (odd), so the result is negative.
3. Using Number Line

A number line can visualize the multiplication of negative numbers:
- Imagine starting at zero. Moving to the left on a number line represents multiplication by a negative number.
- For (-3) * (-2):
- Start at zero.
- Move three units to the left for the first negative 3.
- Then, move another two units to the left for the second negative 2, but since you’re multiplying by a negative, you move to the right twice.
Thus, you land on a positive number.
4. Storytelling
Storytelling can help explain multiplication:
- For instance, imagine you owe someone 5 (-5). If they owe you back 3 three times (-3), you no longer owe them, they owe you. This scenario illustrates (-5) * (-3) = 15.
5. Applying the Commutative Property

The commutative property of multiplication states that a * b = b * a. For negative numbers:
- First, find the absolute value of the numbers.
- Multiply these absolute values.
- Then, apply the sign rule (from method 2).
For example, (-8) * (-4) becomes 8 * 4 = 32, and since the product of two negatives is positive, the final result is 32.
Summing up, understanding how to multiply negative numbers can be simplified with these methods. Each approach, from visual aids to mathematical rules, provides a unique angle to tackle this arithmetic task. Incorporating these strategies can make learning and remembering these operations not only easier but also enjoyable. Instead of a conclusion, consider these tips as your ongoing guide to mastering multiplication with negative numbers, enhancing your mathematical prowess with every step.
What is the sign of the product of two negative numbers?

+
The sign of the product of two negative numbers is always positive.
How does the number of negative signs affect the result in multiplication?

+
An even number of negative signs results in a positive product, while an odd number results in a negative product.
Can I use the commutative property with negative numbers?

+
Yes, the commutative property holds true for multiplication with negative numbers. The order of multiplication does not change the result, though you still need to consider the sign rules.
Why does multiplying two negatives give a positive?

+
This is a convention in mathematics. Multiplying two negatives can be thought of as removing two negative effects, leaving a positive outcome. Conceptually, it can be understood through stories or visual aids.



