5 Essential Tips for Point Slope Form Worksheet Answers
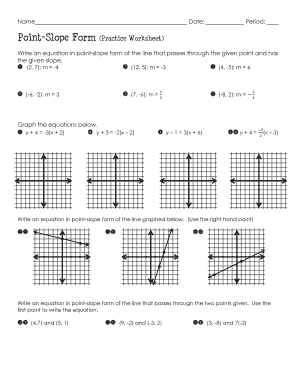
Understanding Point Slope Form in Mathematics

Mathematics often seems like a different language, full of unfamiliar terms and complex equations. Yet, with the right approach, even the most intricate topics can be unraveled. The point-slope form of a line equation is one such topic that frequently leaves students scratching their heads. This blog post offers an exploration into the point-slope form of lines, providing insights into why it's used, how to use it, and what can be learned from it. Here are five essential tips to help you master this concept through worksheet answers:
The Fundamentals of Point Slope Form

Before diving into the tips for solving point-slope form problems, let's understand its basis. The equation of a line in point-slope form is:
y - y1 = m(x - x1)
Where:
- y - y1 represents the difference between the current y-coordinate and the y-coordinate of a known point on the line.
- m is the slope of the line.
- x - x1 is the difference between the current x-coordinate and the x-coordinate of the same known point.
Understanding this equation lays the groundwork for working through point-slope form worksheets effectively.
Tip #1: Identify the Slope and Point Clearly
One of the key aspects of solving problems in point-slope form is correctly identifying the slope and a point on the line. Here's how to do that:
- Look for phrases like "through the point" or "slope is" to find these crucial values.
- Remember that the slope (m) can be positive, negative, zero, or undefined.
- If the problem gives two points but not the slope, use the slope formula:
m = (y2 - y1) / (x2 - x1)
Tip #2: Avoid Common Errors in Application

Application errors are common when working with point-slope form:
- Do not mistakenly use the line's intercepts instead of the given point.
- Be cautious when the slope is negative or when one of the coordinates is zero.
- Ensure you're consistent in substituting the x1 and y1 into the equation.
📝 Note: A common error is confusing the direction of subtraction when calculating the slope or setting up the point-slope equation.
Tip #3: Practice Converting Between Forms

Converting between different forms of line equations is an invaluable skill. Here's how to do it with point-slope form:
- From point-slope to slope-intercept form: Distribute the slope m and solve for y.
- From point-slope to standard form: Rearrange the equation so it is in the format of Ax + By = C.
- Use these conversion skills to cross-check your work and provide alternative solutions.
Converting forms can also help when you're given an equation and need to derive the point and slope.
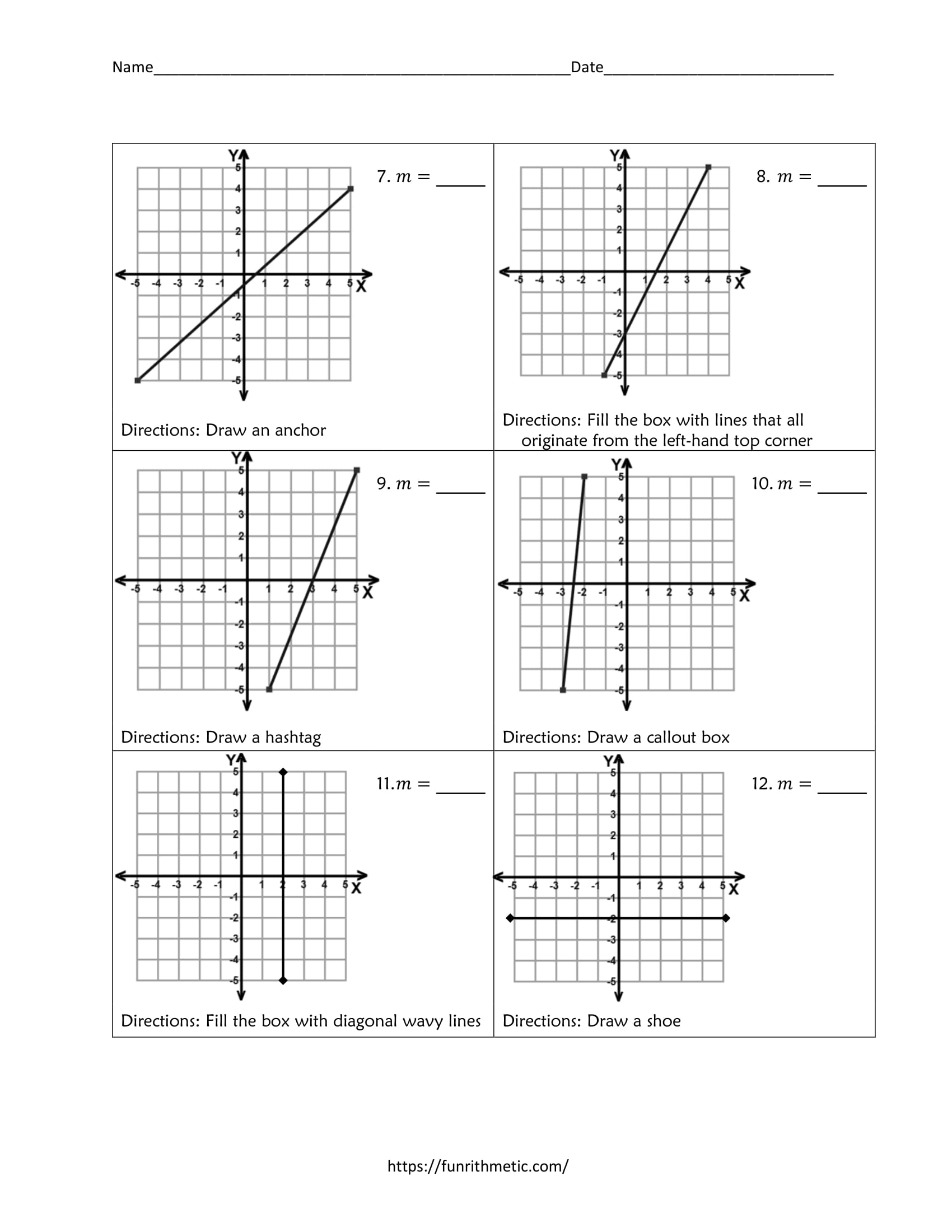
Tip #4: Verify Your Answers Graphically

One of the most reliable methods for checking your work is to graph the line:
- Use a graphing calculator or software to plot the line from your derived equation.
- Ensure the graph passes through the given point and has the correct slope.
- If possible, input the coordinates of another point to see if it aligns with the line on the graph.
Graphical verification provides a visual confirmation of your work, which can be particularly useful in worksheets with multiple problems.
Tip #5: Leverage Algebraic Manipulations

Algebraic manipulation is often necessary when working with point-slope form:
- Isolate terms by simplifying or rearranging the equation.
- Use the distributive property to clear parentheses, where necessary.
- Be aware of when to solve for y, especially if you need the y-intercept or to convert to slope-intercept form.
🖍️ Note: When distributing the slope or subtracting terms, avoid signs errors by paying attention to the signs you're multiplying or dividing.
In conclusion, mastering point-slope form requires a combination of conceptual understanding, practice, and accuracy. By identifying the slope and point, avoiding common errors, converting between forms, verifying graphically, and using algebraic manipulations, you'll be well on your way to tackling any point-slope form problem. Remember that practice makes perfect, and taking the time to work through various problems will solidify your understanding and enhance your skills in both the conceptual and practical aspects of linear algebra.
What is the point-slope form of a line equation?

+
The point-slope form of a line equation is y - y1 = m(x - x1), where m represents the slope of the line and (x1, y1) is a known point on the line.
Why is the point-slope form important?

+
Point-slope form is useful because it allows you to easily write the equation of a line when given the slope and a point, or even when you only have two points and need to find the slope.
Can point-slope form be converted to other forms?

+
Yes, you can convert point-slope form to slope-intercept form by solving for y, and to standard form by rearranging the equation. This conversion is often necessary for comparisons or when working with specific problems.



