5 Proven Ways to Master Multiplying by 2-Digit Numbers
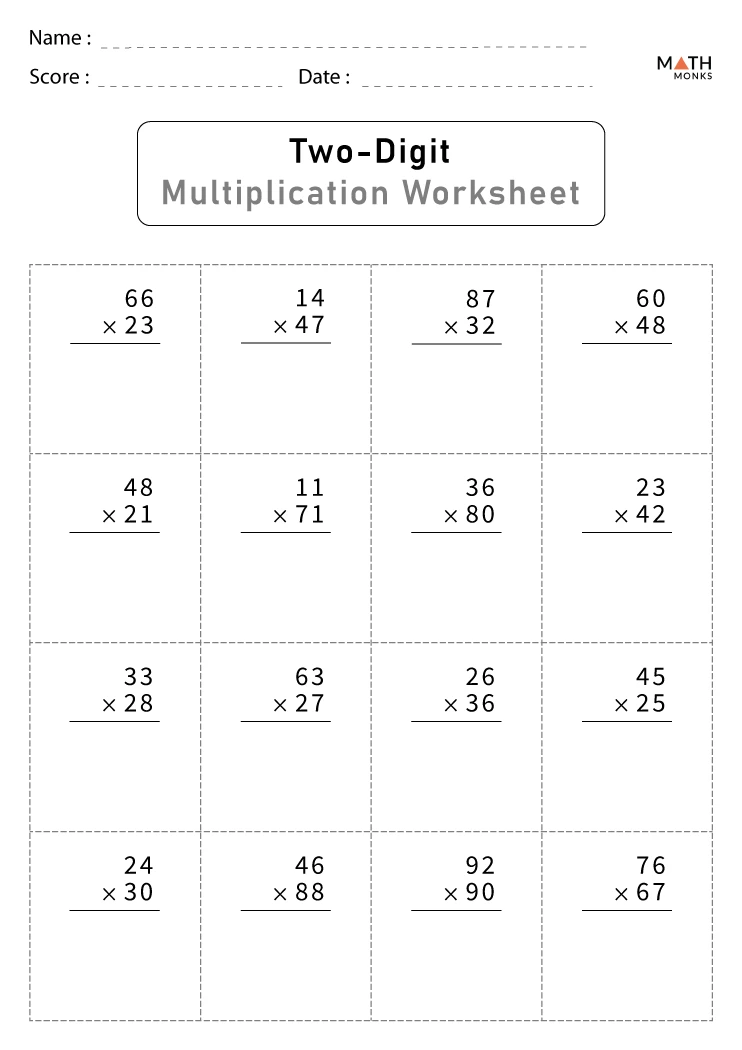
Multiplying by 2-digit numbers can seem daunting at first glance, but with the right strategies and a bit of practice, anyone can master this fundamental arithmetic skill. Whether you're a student looking to improve your math skills, or an adult seeking to sharpen mental arithmetic, this comprehensive guide will introduce you to five proven ways to efficiently multiply by 2-digit numbers.
The Importance of Mental Multiplication
Mastering multiplication by 2-digit numbers isn’t just about schoolwork; it’s a skill that extends to everyday life, from calculating expenses to measuring quantities. Here are some reasons why this skill is indispensable:
- Cost Efficiency: Quick mental calculations help in making instant decisions when shopping or budgeting.
- Time Saving: Learning efficient multiplication methods can drastically reduce the time spent on math problems.
- Cognitive Development: It boosts problem-solving skills, pattern recognition, and overall mental agility.
1. Break Down the Multiplier

One of the most straightforward methods is to break down the 2-digit multiplier into more manageable parts. Here’s how:
- Take a number like 23. Break it down into 20 + 3.
- Now multiply the base number (the first digit of your original number) by these two parts:
- 23 x 7 = (20 x 7) + (3 x 7)
- This simplifies to 140 + 21, which is easily calculated as 161.
⚠️ Note: This method works especially well with numbers that can be easily broken down into multiples of 10.
2. Use The Box Method
The box method, often taught to visualize multiplication, can be an effective visual aid. Here’s how to use it for 2-digit multiplication:
| 6 | 3 | |
|---|---|---|
| 4 | (4 x 6) = 24 | (4 x 3) = 12 |
| 7 | (7 x 6) = 42 | (7 x 3) = 21 |

Add the results within the boxes:
- 24 (from 4 x 6) + 12 (from 4 x 3) + 42 (from 7 x 6) + 21 (from 7 x 3) = 99
3. The Sliding Method

The sliding method involves shifting or “sliding” the digits for easy multiplication:
- Take 14 x 32:
- Multiply 14 by 30 (32 - 2), which is 420.
- Then multiply 14 by the remaining 2, which is 28.
- Add these together: 420 + 28 = 448.
This method uses an intuitive approach to break down the problem into simpler parts.
4. Partial Products

This method breaks multiplication into steps by calculating the products of individual place values:
- Multiplying 56 x 47:
- 50 x 40 = 2000
- 50 x 7 = 350
- 6 x 40 = 240
- 6 x 7 = 42
- Add these results: 2000 + 350 + 240 + 42 = 2632
📝 Note: This method can be particularly useful when teaching multiplication in early education.
5. Lattice Multiplication

Lattice multiplication offers a visual approach where numbers are arranged in a grid:
| 1 | 4 | |
| 7 | ||
| 3 |
- Write 14 and 37 along the grid’s sides.
- Multiply each digit of 14 with each digit of 37, splitting the product into tens and units. For instance, for 7 x 1, write 7; for 3 x 4, write 12 (1 and 2).
- Now, sum the numbers along the diagonals to get the final product.
To conclude, mastering the multiplication by 2-digit numbers isn't just about learning mathematical operations. It's about understanding patterns, enhancing cognitive function, and making daily calculations more manageable. The five methods we've explored offer different ways to approach multiplication, each with its own advantages. Whether you favor visual aids like the lattice or box methods, or the logical breakdown techniques like partial products or sliding, consistent practice with these strategies will boost your mental math capabilities.
Why is it beneficial to learn different multiplication methods?

+
Learning various methods allows flexibility in problem-solving and caters to different learning styles, enhancing overall understanding and efficiency in calculations.
Which method is best for quick mental calculations?

+
The sliding method or breaking down the multiplier often allows for quicker mental arithmetic as they leverage familiar and simple calculations.
Can these methods help in division as well?

+
Yes, understanding multiplication can indeed help with division, as division is essentially reverse multiplication. However, certain techniques might need to be adapted for division.
Are there any online tools or apps that practice these methods?

+
There are numerous math apps and websites offering interactive lessons and practice sessions for various multiplication methods, tailored to different age groups.
What if I struggle with these methods?

+
Struggling initially is normal. Persistent practice, visual aids, or seeking help from a tutor or educational resources can make a significant difference.



