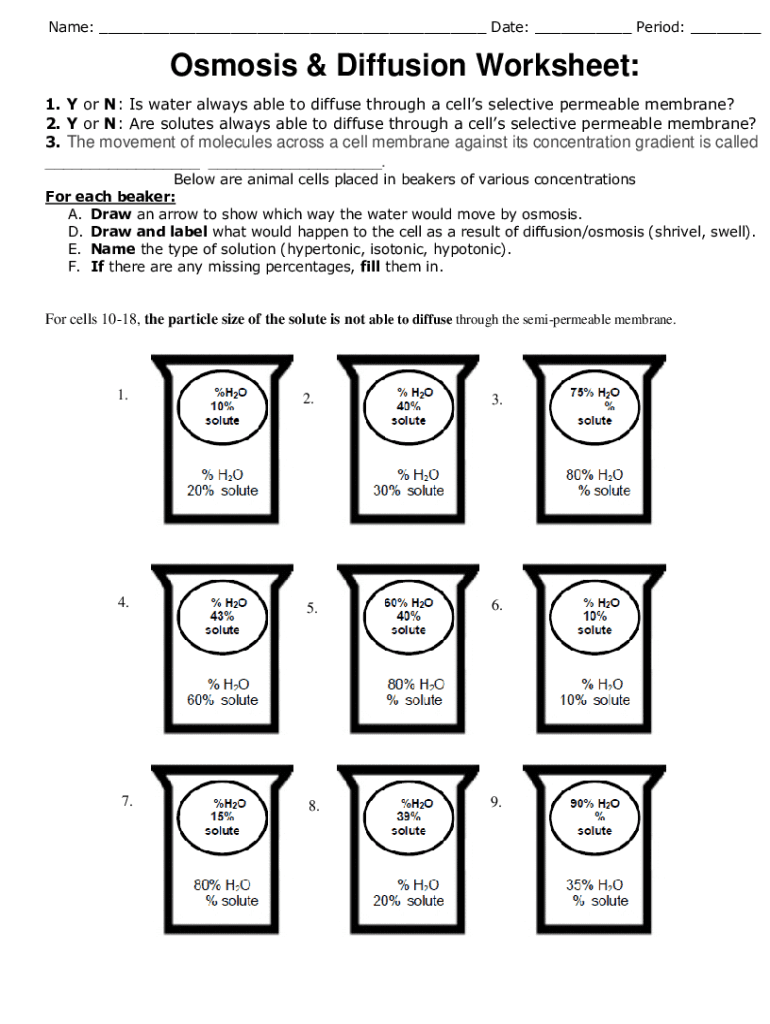
Multi-Step Equations With Fractions: Worksheet Guide

Are you struggling with multi-step equations involving fractions? You're not alone. Many students find this topic challenging, but it's a crucial skill in algebra, impacting everything from chemistry equations to financial planning. This guide is designed to walk you through the steps, offer practical examples, and help you master these equations.
Understanding Multi-Step Equations with Fractions

Before diving into solving, let’s ensure we understand what we’re dealing with. Multi-step equations include:
- Variables on both sides of the equation
- Multiple operations like addition, subtraction, multiplication, or division
- Fractions, which require an extra layer of manipulation
The goal is to isolate the variable, often denoted as ‘x’.

Solving Multi-Step Equations with Fractions

Here are the steps to solve these equations:
Step 1: Eliminate the Fractions

The first step in dealing with fractions in multi-step equations is to eliminate them. This is done by finding the Least Common Multiple (LCM) of the denominators and multiplying each term in the equation by this LCM. This action simplifies the equation and helps avoid mistakes with fractions:
- Identify all denominators in the equation.
- Determine the LCM of these denominators.
- Multiply each term of the equation by this LCM.
💡 Note: By removing fractions early, you reduce the chance of errors as the equation becomes easier to manage.
Step 2: Distribute and Combine Like Terms

After eliminating fractions, your next move is to distribute multiplication over addition or subtraction if parentheses are present, and then combine like terms:
- Distribute the LCM to any terms within parentheses.
- Combine like terms to simplify the equation further.
Step 3: Isolate the Variable

Now, isolate the variable:
- Move all constants to one side of the equation.
- Move all terms with the variable to the other side.
- Simplify the equation to express the variable on one side.
Step 4: Solve for the Variable

After isolating the variable:
- Perform any remaining operations to find the variable’s value.
Step 5: Check Your Solution

Finally, substitute the value you’ve found back into the original equation to ensure it balances:
- Plug in the solution for the variable.
- Verify that both sides of the equation are equal.
🧐 Note: Checking your solution is vital to ensure there were no errors in your calculation or simplification steps.
Worksheet Examples

To solidify your understanding, let’s go through a few examples. These will demonstrate how to apply the steps:
Example 1

Solve the equation: 3/4x + 2⁄3 = 5⁄6
- The LCM of 4, 3, and 6 is 12. Multiply each term by 12:
3⁄4*12x + 2⁄3*12 = 5⁄6*12leading to9x + 8 = 10. - Isolate x: subtract 8 from both sides, then divide by 9.
- The solution is
x = 1⁄5.
Example 2

Solve the equation: 1/3x - 1⁄4 = 1/6x + 2⁄5
- The LCM of 3, 4, 6, and 5 is 60. Multiply each term by 60:
20x - 15 = 10x + 24. - Move x terms and constants:
20x - 10x = 24 + 15. - Simplify:
10x = 39leading tox = 3.9.
These examples show the importance of meticulous calculation, particularly when dealing with fractions.
Common Pitfalls and How to Avoid Them

When working with multi-step equations involving fractions, be aware of these common mistakes:
- Incorrect LCM: Always double-check your LCM, as using the wrong one can lead to incorrect simplification.
- Distributing Errors: Ensure you distribute multiplication correctly through parentheses or fractions.
- Combining Terms: Only combine like terms, as different variables or numbers with different powers cannot be combined.
- Transcription Errors: Be diligent when writing down or copying equations to avoid missteps.
By avoiding these common pitfalls, you'll be well on your way to solving multi-step equations with ease.
Mastering multi-step equations with fractions involves understanding the foundational steps, practicing with varied examples, and being mindful of common errors. With patience and practice, these equations will become second nature. Remember, algebra is a language, and the more you speak it, the more fluent you'll become. Now, go forth, and solve those equations with confidence!
What if the LCM is not obvious?

+
Use prime factorization to find the LCM. If you’re stuck, start with the largest denominator and adjust as needed.
Can these steps be applied to equations with negative fractions?
+
Absolutely! Just make sure to account for the sign when combining or distributing.
What if the equation is unsolvable?

+
There might be scenarios where equations don’t have a solution (inconsistent) or have infinite solutions (identity). Double-check your steps and your original equation to confirm.
How can I check my work efficiently?
+Keep track of your steps, especially after eliminating fractions, and always substitute your solution back into the original equation to ensure it balances.
What if I find a different LCM than my teacher?
+If your LCM is different, it might still work, but the teacher might have selected an LCM that simplifies subsequent steps more easily.