5 Mole Practice Problems and Answers Revealed

In the world of chemistry, understanding how to work with moles is fundamental. Whether you're preparing for an exam or just trying to solve a daily problem related to chemical calculations, mastering mole concepts can be immensely beneficial. Today, we're diving into 5 mole practice problems that will help you sharpen your skills. These problems cover various aspects of mole calculations, including conversions between moles, mass, volume of gases, and more.

Problem 1: Converting Mass to Moles

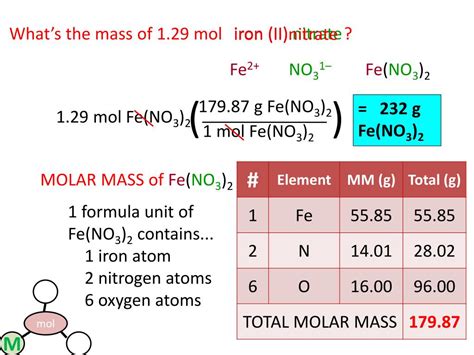
Suppose you have 20 grams of calcium carbonate (CaCO₃). How many moles does this equate to?

• First, find the molar mass of CaCO₃:
  • Ca: 40.08 g/mol
  • C: 12.01 g/mol
  • O: 16.00 g/mol (x3 for 3 oxygen atoms)
  • Total: 40.08 + 12.01 + (16.00 x 3) = 100.09 g/mol
• Convert the mass to moles: \[ \text{Moles} = \frac{\text{Mass}}{\text{Molar Mass}} = \frac{20 \text{ g}}{100.09 \text{ g/mol}} \approx 0.200 \text{ moles} \]

Problem 2: Converting Volume of Gas to Moles

Calculate the number of moles in 2.5 liters of oxygen gas (O₂) at STP.

• At STP, one mole of an ideal gas occupies 22.4 liters.
• Use the relationship: \[ \text{Moles} = \frac{\text{Volume at STP}}{22.4 \text{ L/mol}} = \frac{2.5 \text{ L}}{22.4 \text{ L/mol}} \approx 0.112 \text{ moles} \]

Problem 3: Using Avogadro's Number

How many molecules are in 0.5 moles of glucose (C₆H₁₂O₆)?

• Using Avogadro's number (6.022 x 10²³ molecules/mole): \[ \text{Number of molecules} = \text{Moles} \times 6.022 \times 10^{23} = 0.5 \times 6.022 \times 10^{23} = 3.011 \times 10^{23} \text{ molecules} \]

Problem 4: Finding Molarity from a Solute Concentration

A solution is made by dissolving 58.44 grams of sodium chloride (NaCl) in enough water to make 1 liter of solution. What is the molarity?

• The molar mass of NaCl is approximately 58.44 g/mol.
• Molarity is moles of solute per liter of solution: \[ \text{Molarity} = \frac{\text{Moles of NaCl}}{1 \text{ L}} = \frac{1 \text{ mole}}{1 \text{ L}} = 1 \text{ M} \]

Problem 5: Mole Ratio and Mass Calculations

In the combustion of propane (C₃H₈), the equation is:

C₃H₈ + 5O₂ → 3CO₂ + 4H₂O. How much O₂ is needed to completely burn 5 moles of propane?

• From the balanced equation, the mole ratio of C₃H₈ to O₂ is 1:5.
• Therefore, for 5 moles of C₃H₈: \[ \text{Moles of O}_2 = 5 \times 5 = 25 \text{ moles} \]

🔬 Note: Ensure to use the correct units when performing conversions, as units play a crucial role in accuracy.

These mole practice problems have covered several key calculations you'll encounter in chemistry. They illustrate how moles can be used to understand both macroscopic properties like mass and volume, as well as microscopic aspects like the number of molecules or atoms. Practicing these types of problems will not only improve your understanding of the mole concept but also enhance your ability to handle various chemical calculations with confidence.

What are moles used for in chemistry?

+

Moles are a fundamental unit in chemistry that allows us to count atoms, molecules, or ions in a given substance. They’re used to relate the mass of a substance to the number of atoms or molecules it contains, enabling chemists to determine reaction stoichiometry, concentration, and other properties.

Why is it important to convert between moles and mass?

+

Converting between moles and mass is critical for precise chemical reactions, where the exact amount of reactants is crucial. It helps in understanding how much of each chemical is required or produced in a reaction, ensuring efficiency and preventing waste.

How can I use Avogadro’s number in calculations?

+

Avogadro’s number (6.022 x 10²³) is used to convert from moles to the number of entities (atoms, molecules, etc.). For example, if you have 1 mole of any substance, Avogadro’s number tells you how many individual particles that mole contains.