5 Ways to Master Mixed Numbers with Worksheets

Mixed numbers are a fundamental concept in mathematics, particularly when dealing with fractions. Understanding mixed numbers not only simplifies arithmetic operations but also aids in real-world applications where measurements and quantities often don't fit neatly into whole numbers. If you're looking to master mixed numbers, incorporating practice through worksheets can significantly enhance your proficiency. Here are five effective strategies to conquer mixed numbers using worksheets:
1. Understanding the Basics

Before diving into complex operations with mixed numbers, it’s crucial to grasp the basics:
- Definition: A mixed number consists of a whole number part and a fractional part. For example, 2 ¼ where 2 is the whole number and ¼ is the fraction.
- Conversion: Convert mixed numbers to improper fractions or vice versa. To convert 2 ¼ to an improper fraction, multiply the whole number (2) by the denominator (4) and add the numerator (1) to get 9⁄4.
Worksheets can help solidify this understanding:
- Create worksheets that include exercises where students convert between mixed numbers and improper fractions.
- Incorporate visual aids like diagrams or number lines to visualize the relationship between whole numbers and fractions.
📊 Note: Using visual aids like fraction strips or pie charts can make the conversion process more intuitive for students.
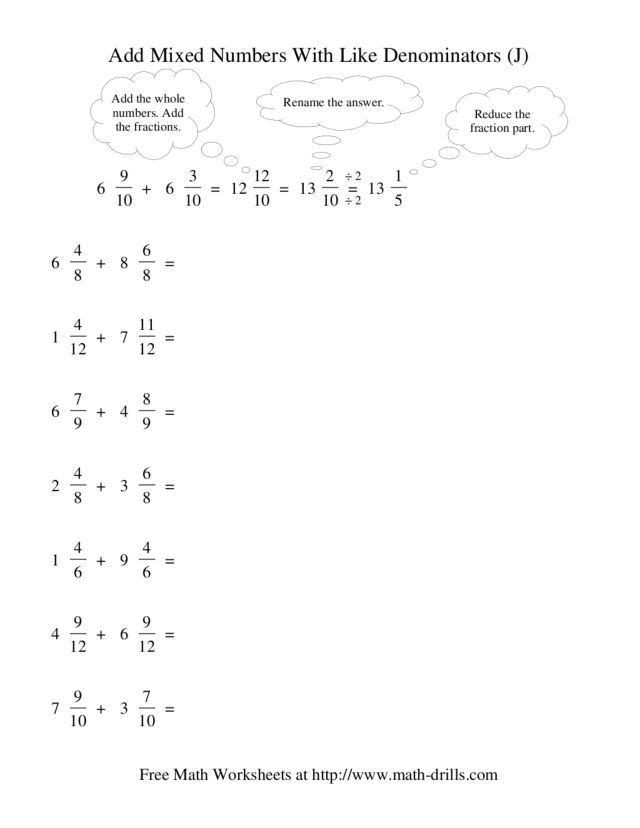
2. Addition and Subtraction

Addition and subtraction of mixed numbers can be tricky due to the need to align the denominators:
- Worksheets should start with simpler problems where one fraction needs to be converted to have the same denominator as the other.
- Move to more complex scenarios where borrowing or regrouping is necessary. For example:
Problem Step by Step 3 ¾ - 2 ½ 1. Convert 3 ¾ to an improper fraction:
3 * 4 + 3 = 15, so 15⁄4.
2. Convert 2 ½ to an improper fraction:
2 * 2 + 1 = 5, so 5⁄2.
3. Find a common denominator (4 in this case).
4. Subtract 5⁄2 from 15⁄4 (after adjusting 5⁄2 to 10⁄4):
15⁄4 - 10⁄4 = 5⁄4 or 1 ¼
3. Multiplication and Division

Mastery of multiplication and division with mixed numbers involves:
- Converting mixed numbers to improper fractions before performing operations.
- Using worksheets to practice these conversions alongside multiplication or division. For example:
- (3 ½) * (2 ⅔):
- Convert both to improper fractions: 7⁄2 * 8⁄3.
- Multiply: (7 * 8) / (2 * 3) = 56⁄6, which simplifies to 9 ⅓.
- (3 ½) * (2 ⅔):
4. Real-World Applications
Applying mixed numbers in real-life scenarios:
- Incorporate word problems in worksheets where mixed numbers are part of measurements, recipes, or practical tasks.
- For instance, ask students to calculate how much paint is needed for a room, considering dimensions in mixed numbers.
5. Sequential Complexity

Incrementally increasing the complexity of exercises:
- Start with basic operations and progressively introduce mixed number operations in sequences or in larger problem sets.
- Use color-coded worksheets where the difficulty level increases visually, helping students recognize and prepare for tougher problems.
🎯 Note: Worksheets with mixed sets of problems help students understand the context of mixed numbers in varied mathematical problems.
In summary, mastering mixed numbers involves understanding their basic structure, converting between different forms, and applying operations accurately. Worksheets that cover these aspects, from visual aids for conversion to real-world applications and sequential problem-solving, play a crucial role in developing this understanding. The consistent practice through well-designed worksheets can turn the complexities of mixed numbers into familiar, manageable tasks.
Why should we learn mixed numbers?

+
Mixed numbers reflect real-life quantities where whole numbers are often not sufficient. Understanding them helps in practical scenarios like cooking, carpentry, or measurements, where precision is necessary.
How do worksheets benefit learning mixed numbers?

+
Worksheets provide structured practice, reinforce concepts through repetition, and allow for mistakes in a low-pressure environment, which is crucial for mastering mixed numbers.
Can mixed numbers only be used with fractions?

+
While mixed numbers are most commonly associated with fractions, the concept can extend to decimals, percentages, or even units in physics where partial values are represented alongside whole values.



