5 Essential Tips for Adding and Subtracting Scientific Notation

The Basics of Scientific Notation
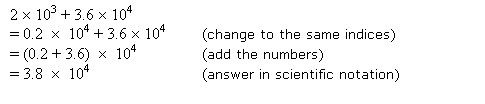
Scientific notation, or standard form, is a way of expressing numbers that are too large or too small to be conveniently written in decimal form. It is commonly used by scientists, mathematicians, and engineers to manage very small or large numbers. Understanding how to add and subtract using scientific notation is fundamental for anyone in a technical field or involved in scientific research.

Tip 1: Normalize the Exponents

The first step when adding or subtracting numbers in scientific notation is to ensure that the exponents are the same. Here is how you can do it:
- Identify the smallest exponent and adjust all other exponents to match it.
- Adjust the coefficient (the part before the times 10 to the power) accordingly to maintain the value of the number.
🔍 Note: When adjusting the coefficient, remember that each shift in the decimal point represents a change of one in the exponent. For example, moving the decimal one place to the right means increasing the exponent by one, and moving it to the left means decreasing it by one.
Tip 2: Combine the Coefficients

Once the exponents are the same, proceed to combine the coefficients:
- If you are adding, simply add the coefficients.
- If you are subtracting, subtract the coefficients.
- Keep the exponent the same for the resulting number.
Tip 3: Ensure Proper Rounding

Scientific notation often requires rounding to maintain a manageable number of significant figures. Here are some guidelines:
- Count the number of significant figures in your original numbers.
- After the operation, round the result to match the least number of significant figures from the operands.
💡 Note: Significant figures provide an insight into the precision of measurements, which is crucial in scientific work.
Tip 4: Use Notation Tools

While learning to add and subtract numbers in scientific notation manually is beneficial, various tools can simplify this process:
- Scientific calculators are excellent for quick computations, ensuring accuracy with many digits.
- Online calculators and software specifically designed for handling scientific notation can be very helpful.
Here is a simple table to help choose the right tool:
| Tool | Benefits |
|---|---|
| Scientific Calculator | Portable, fast, and precise. Suitable for on-the-go calculations. |
| Online Calculator | Accessible from any device, often with visual step-by-step explanations. |
| Software | Can handle complex operations, integration with other scientific tools, and data manipulation. |

Tip 5: Practice with Examples

The best way to become proficient in adding and subtracting in scientific notation is through practice. Here are some examples to guide you:
Example 1: Addition

- Add (4.2 × 103) and (6.9 × 102):
- Convert 6.9 × 102 to 0.69 × 103.
- Add the coefficients: 4.2 + 0.69 = 4.89.
- Result: 4.89 × 103.
Example 2: Subtraction

- Subtract (8.5 × 105) from (3.5 × 106):
- Convert 8.5 × 105 to 0.85 × 106.
- Subtract the coefficients: 3.5 - 0.85 = 2.65.
- Result: 2.65 × 106.
📝 Note: Always ensure you check your work against actual measurements or simulations to verify accuracy in scientific calculations.
Understanding how to add and subtract in scientific notation is vital not just for the sake of convenience but also for maintaining accuracy in scientific and engineering work. By normalizing exponents, combining coefficients, rounding appropriately, using the right tools, and practicing with real-world examples, you can master this essential skill. Remember, proficiency comes with practice, so keep experimenting and refining your techniques to handle these operations seamlessly.
Why do we use scientific notation?

+
Scientific notation is used to express very large or very small numbers in a compact form, making them easier to work with, especially in scientific calculations and data representation.
How do I know if my result is in proper scientific notation?

+
A number is in proper scientific notation if the coefficient is between 1 and 10 (inclusive of 1 but less than 10), followed by a power of 10, with all significant figures properly rounded.
Can I add numbers with different exponents without converting them?

+
No, you must convert the exponents to be the same before adding or subtracting the coefficients to ensure the operations are mathematically correct.