5 Ways to Simplify Mixed Numbers and Improper Fractions

In mathematics, understanding how to work with fractions is crucial, particularly for simplifying mixed numbers and improper fractions. Whether you're teaching someone or brushing up on your own skills, knowing the ins and outs of these techniques can streamline mathematical operations significantly. Here are five effective methods to simplify mixed numbers and improper fractions:
Method 1: Conversion to an Improper Fraction

The first step in simplifying fractions often involves converting mixed numbers to improper fractions. This is particularly useful for performing operations like addition and subtraction.
- Multiply the whole number part by the denominator of the fraction part.
- Add the numerator to this result.
- Place the sum over the original denominator.
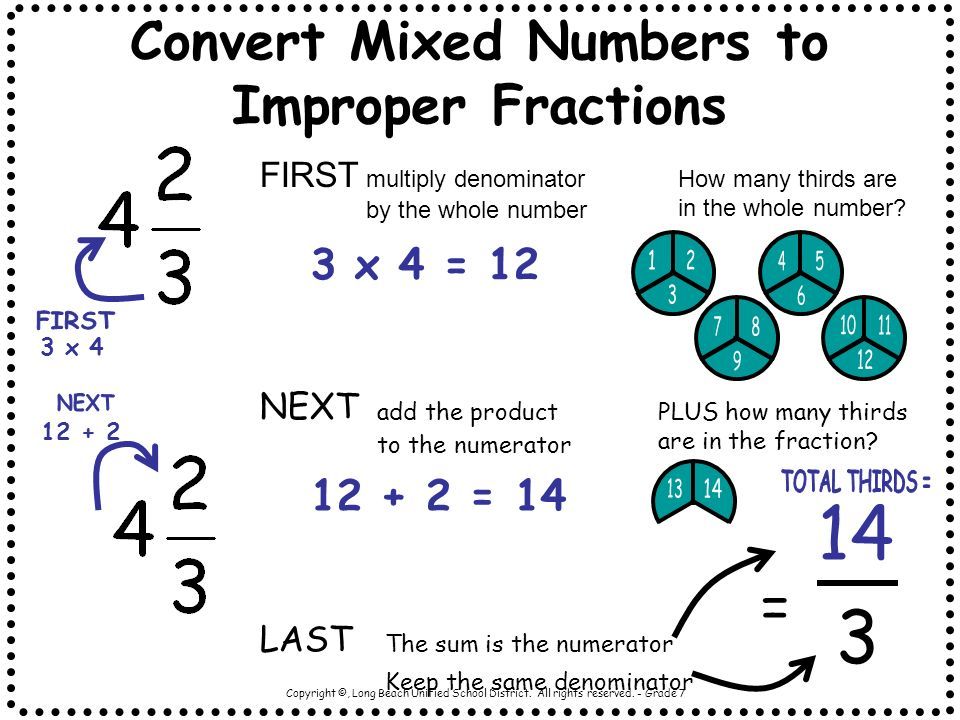
Example: Convert 2 ¾ to an improper fraction.
| Step | Calculation |
|---|---|
| Multiply the whole number by the denominator: | 2 × 4 = 8 |
| Add this result to the numerator: | 8 + 3 = 11 |
| The improper fraction is: | 11⁄4 |

📝 Note: When dealing with operations like multiplication or division, converting a mixed number to an improper fraction is key because it makes the process more straightforward.
Method 2: Simplifying Improper Fractions
Once you have an improper fraction, the next step is to simplify it. Simplifying fractions reduces them to their lowest terms, making them easier to work with and understand:
- Identify the common factors of the numerator and the denominator.
- Divide both the numerator and the denominator by their greatest common divisor (GCD).
Example: Simplify 11⁄4.
- The GCD of 11 and 4 is 1 since 11 is a prime number.
- Therefore, 11⁄4 remains as is since they share no common factors other than 1.
📌 Note: Not all improper fractions can be simplified, but knowing the process can help with conceptual understanding and practice.
Method 3: Back to a Mixed Number
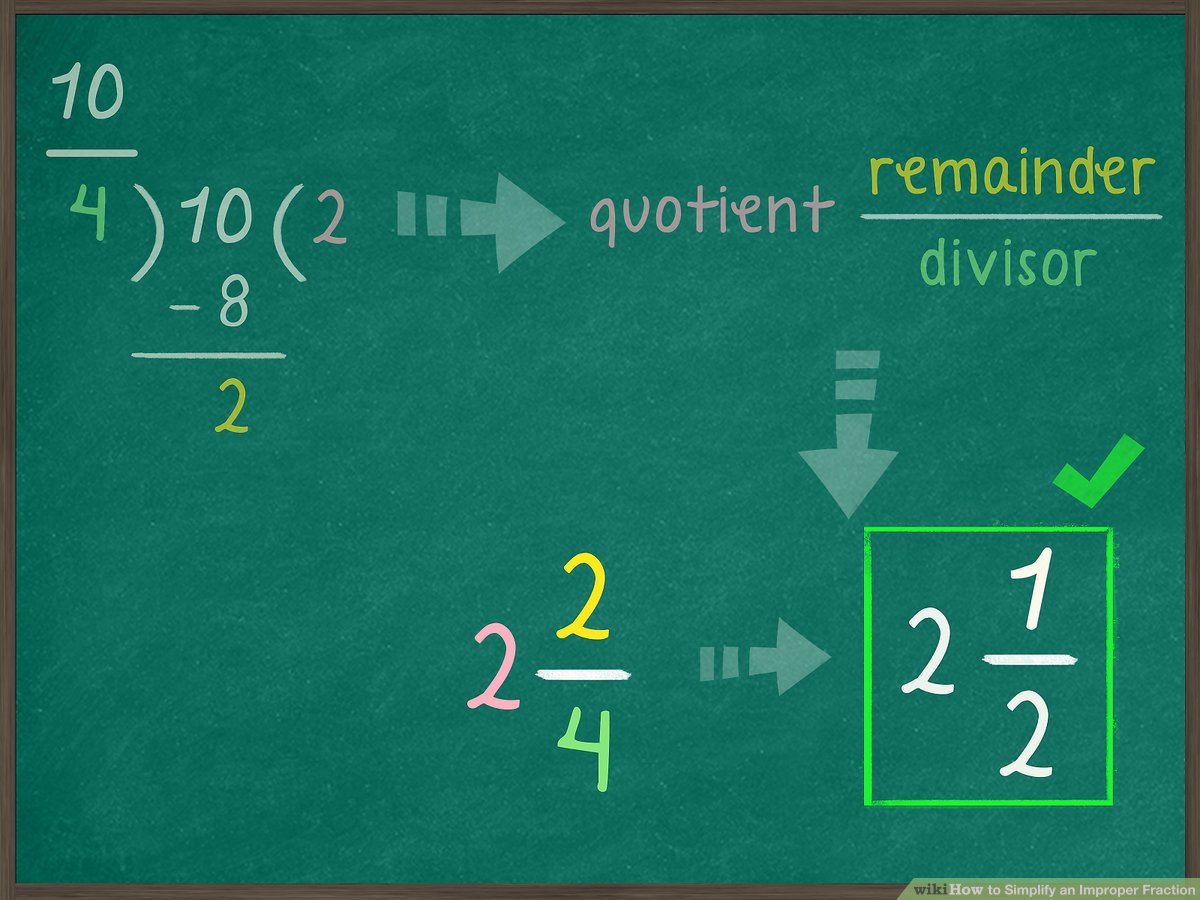
After simplifying an improper fraction, it might be useful to convert it back to a mixed number for better readability or to align with the problem’s requirements:
- Divide the numerator by the denominator.
- The whole number quotient becomes the whole number part.
- The remainder becomes the new numerator over the same denominator.
Example: Convert 11⁄4 back to a mixed number.
- 11 divided by 4 gives a quotient of 2 with a remainder of 3.
- The mixed number is 2 ¾.
Method 4: Using Visual Aids

For those who are visual learners, using diagrams or pie charts can provide a clear understanding:
- Draw a circle to represent the whole.
- Divide the circle into equal parts corresponding to the denominator.
- Shade in the parts that represent the numerator.
This method is particularly effective for kids or for visualizing the fraction in a physical form.
Method 5: Fraction Strips or Cuisenaire Rods

Another hands-on approach is to use fraction strips or Cuisenaire rods:
- Fraction strips are pre-cut strips that show various fractions of a whole.
- Cuisenaire rods come in different lengths, each representing a fraction when compared to the longest rod.
By arranging these rods or strips, you can match the improper fraction to its equivalent mixed number or see the proportions clearly.
Wrapping up, the ability to simplify mixed numbers and improper fractions is not just a skill for solving equations; it's about developing a deeper understanding of numbers and how they interact. Each method described above offers a different perspective on fractions, aiding in teaching, learning, or simply refining one's mathematical prowess. From conversion to visualization, these techniques make the once daunting task of fraction simplification more accessible and intuitive, ensuring that everyone can approach math with confidence.
Why do I need to simplify fractions?

+
Simplifying fractions makes arithmetic operations easier, and it also helps in understanding the true relationship between numbers. It’s about reducing complexity and making calculations straightforward.
What if both the numerator and denominator of my fraction are even numbers?

+
If both are even, you can always divide both by 2 to simplify. Keep dividing by 2 until one or both are odd or the fraction can’t be simplified further.
Can I convert an improper fraction back to a mixed number mentally?

+
With practice, yes. You divide the numerator by the denominator in your head, noting the remainder as the new numerator for the fraction part.



