5 Ways to Master Slope Calculation with Ease

Understanding the slope of a line is essential in various fields, from construction to engineering, finance, and even daily life. Slope calculation is not only a fundamental aspect of algebra but also crucial in real-world applications where understanding the steepness or incline of a line or surface can lead to more informed decisions. Let's dive into five straightforward and effective methods to master the calculation of slope, each tailored for ease of use and understanding.
1. Using the Slope Formula

The basic formula to calculate the slope of a line is:
m = (y2 - y1) / (x2 - x1)
Where:
- m represents the slope of the line.
- (x1, y1) are the coordinates of the first point.
- (x2, y2) are the coordinates of the second point.
📌 Note: Ensure both points are on the same straight line.
To apply this:
- Identify two points on your line or graph.
- Plug these coordinates into the formula.
- Calculate the difference in the y-coordinates and the x-coordinates separately.
- Finally, divide the result from the y-coordinates by that of the x-coordinates.
2. Rise Over Run Visualization

The concept of "rise over run" is a visual approach to understanding slope:
- Rise: This is the vertical change or difference in y-coordinates between two points.
- Run: This is the horizontal change or difference in x-coordinates between two points.
🗺️ Note: "Rise over Run" can be visualized by counting how many units up or down ("rise") and then how many units left or right ("run").
Here's how you can apply it:
- Draw your line on graph paper.
- Count the squares you move vertically from one point to another for the rise.
- Similarly, count the squares horizontally for the run.
- The slope is the rise divided by the run.
3. Using Technology for Accuracy

In today's digital age, technology has made slope calculation more accessible:
- Graphing Calculators: Use functions to input equations or points directly.
- Online Slope Calculators: Websites where you can enter points to find the slope instantly.
- Spreadsheet Software: Excel or Google Sheets can compute slopes using functions like LINEST.
| Tool | Example |
|---|---|
| Graphing Calculator | y = 2x + 3 |
| Online Calculator | Input: Point (1, 3) and Point (4, 9) |
| Spreadsheet Software | =SLOPE(B2:B10, A2:A10) |

4. Graphical Analysis
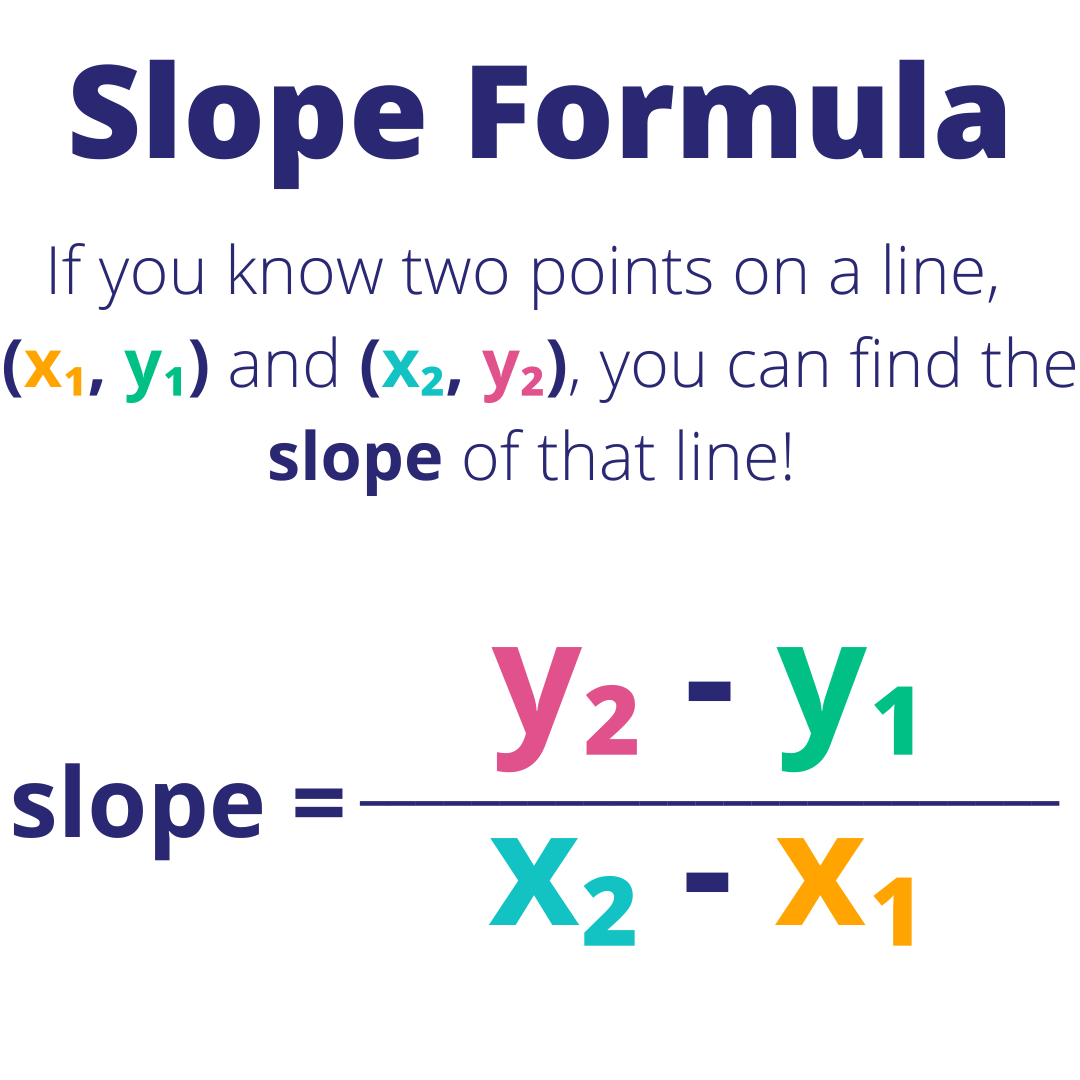
Graphical analysis involves plotting points on a graph and visually determining the slope:
- Plot your points on a coordinate grid.
- Draw a line passing through these points.
- Count the units for rise and run, keeping in mind the direction of movement.
- Calculate the slope.
This method helps you understand the geometric relationship of the slope directly from the line's appearance.
5. Understanding Positive, Negative, Zero, and Undefined Slopes

Here's a quick reference to different types of slopes:
| Type | Appearance | Characteristic |
|---|---|---|
| Positive Slope | Slants Upwards | Up as we move right |
| Negative Slope | Slants Downwards | Down as we move right |
| Zero Slope | Horizontal Line | No vertical change |
| Undefined Slope | Vertical Line | Infinite steepness |
Mastering these concepts will enhance your ability to interpret various slopes and apply them in practical scenarios.
To recap, mastering slope calculation involves understanding its formula, visualizing it with "rise over run," leveraging technology for precision, performing graphical analysis, and recognizing different slope types. This knowledge not only enriches your mathematical skills but also applies directly to real-world problems. With these techniques in hand, you'll be well-equipped to tackle any situation requiring slope calculation with confidence and ease.
What is the slope of a line used for?
+
Slope is used to measure the steepness or incline of lines in various fields, helping to determine how a variable changes with respect to another, calculate road gradients, design structures, analyze financial trends, and more.
Can slope be negative?

+
Yes, slope can be negative. A negative slope indicates that the line is decreasing, meaning the y-value decreases as the x-value increases.
What does a slope of zero mean?

+
A slope of zero indicates a horizontal line, where there is no vertical change in the y-coordinate for any horizontal movement in the x-coordinate.