5 Essential Tips for Finding Missing Angles

Understanding geometry often boils down to grasping a few fundamental principles, and finding missing angles in various figures is one of the core skills any student needs to master. Whether you're solving for angles in triangles, quadrilaterals, or circles, these skills pave the way for proficiency in advanced math. Here's a guide to help you find those elusive angles with ease:
The Basics of Angle Measurement

Before diving into angle finding techniques, it’s crucial to comprehend how angles are measured:
- Angles are measured in degrees (°), minutes (‘), and seconds (“). There are 360 degrees in a full circle.
- Types of angles include: acute (less than 90°), right (exactly 90°), obtuse (between 90° and 180°), straight (exactly 180°), and reflex (more than 180° but less than 360°).
🔎 Note: Angles in a straight line add up to 180°, while angles around a point add up to 360°.
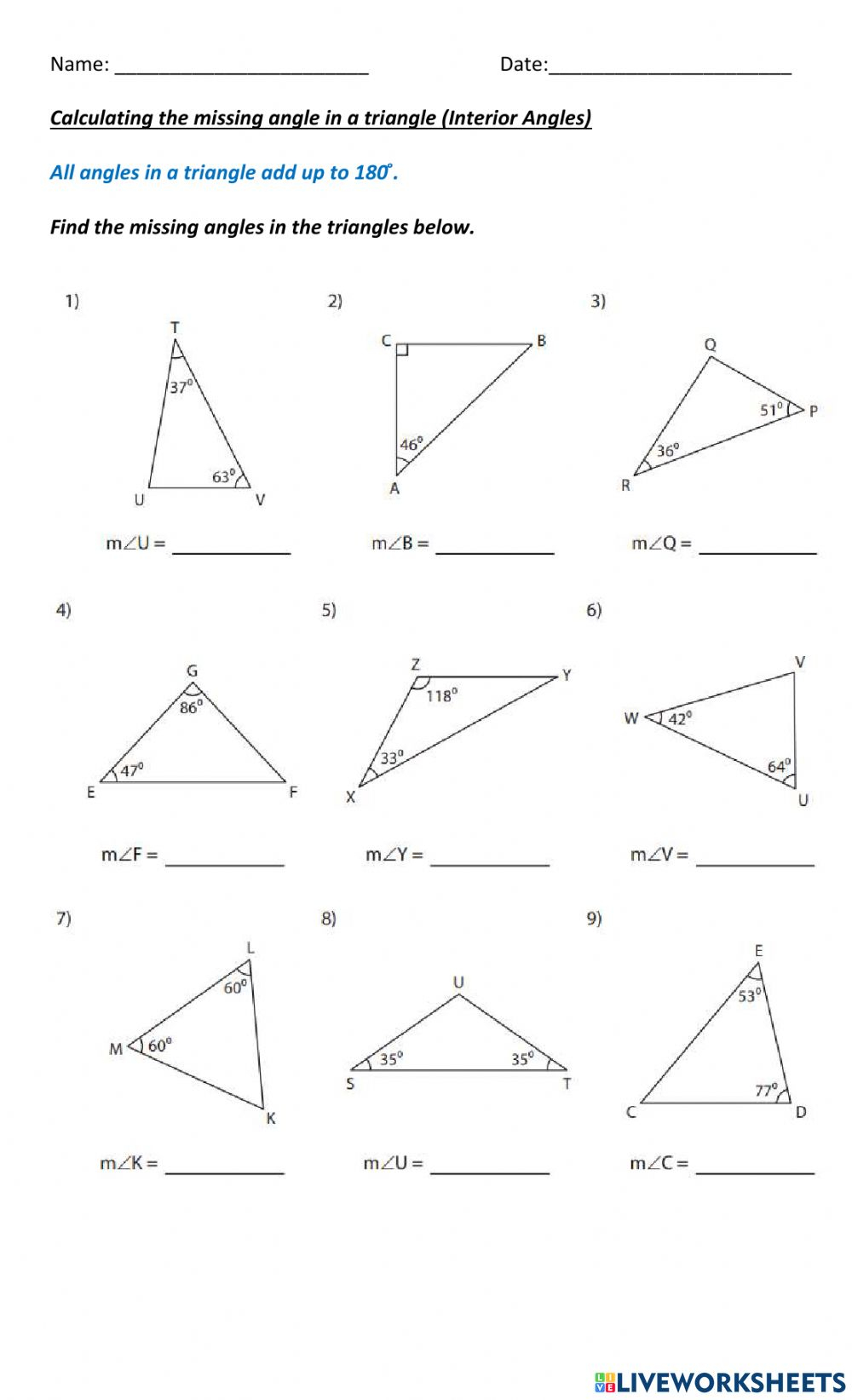
1. Use the Sum of Angles in Polygons

One of the simplest yet most effective ways to find missing angles is by leveraging the properties of polygons:
- For a triangle, all angles sum to 180°. If you know two angles, subtract their sum from 180 to find the third.
- Quadrilaterals have angles summing to 360°. Knowing three angles allows you to find the fourth by subtraction.
- For polygons with more than four sides, use the formula: (n-2) × 180, where ‘n’ is the number of sides, to find the sum of interior angles.
Here’s a simple table to illustrate this:
| Polygon | Sum of Interior Angles |
|---|---|
| Triangle | 180° |
| Quadrilateral | 360° |
| Pentagon | 540° |
2. Apply Trigonometry

When dealing with right triangles, trigonometry is your friend. Here are the key formulas:
- Sine (sin): Opposite over hypotenuse.
- Cosine (cos): Adjacent over hypotenuse.
- Tangent (tan): Opposite over adjacent.
Example: If you know the length of two sides, use the inverse trigonometric functions to find an angle:
- sin⁻¹(opposite/hypotenuse) = angle
- cos⁻¹(adjacent/hypotenuse) = angle
- tan⁻¹(opposite/adjacent) = angle
📐 Note: SOHCAHTOA is a mnemonic that can help you remember these relationships.
3. Parallel Lines and Transversals

Angles formed by parallel lines cut by a transversal provide another set of relationships:
- Corresponding angles are congruent.
- Alternate interior and exterior angles are congruent.
- Consecutive interior angles are supplementary.
Here’s how to find a missing angle:
- If you know one angle created by the transversal, find its corresponding or alternate angle.
- Subtract supplementary angles from 180°.
By understanding these properties, you can solve for unknown angles without relying solely on measurements.
4. Use Circle Properties

Circle geometry introduces its own set of rules for angle finding:
- Inscribed Angles: An angle inscribed in a circle is half the measure of the arc it intercepts.
- Central Angles: The measure of a central angle is equal to the measure of the arc it intercepts.
- Opposite Angles: Angles at the circumference subtended by the same arc are equal.
🌐 Note: A semicircle always has an inscribed angle of 90°.
5. Angle-Chasing

Often referred to as “angle hunting,” this method involves using the relationships between different angles in a geometric figure:
- Start with known angles or simple relationships like vertical or supplementary angles.
- Use the theorems and properties from polygons, circles, and parallel lines to solve for unknown angles step by step.
Angle-chasing requires patience and a deep understanding of geometric theorems. Here’s an example:
- Identify a pair of supplementary angles formed by a transversal cutting parallel lines.
- Use the angles within a triangle to find other angles.
- Apply the properties of inscribed angles or central angles in a circle.
Angles are not just numbers; they are the keys to unlocking the complexity of shapes and spaces. Whether you're struggling with basic geometry or diving into higher-level mathematics, mastering these tips will give you a solid foundation:
- Remember the sum of angles in polygons.
- Leverage trigonometry for right triangles.
- Utilize properties of parallel lines and transversals.
- Understand circle properties for angles at the circumference.
- Practice angle-chasing to piece together geometric puzzles.
By internalizing these principles and practicing with real problems, you'll find that missing angles become less daunting, turning geometric puzzles into solvable equations. Geometry, much like art, has its own beauty in its logical structure, and mastering the art of finding angles is one of the steps towards appreciating that structure.
What is the sum of the interior angles of a hexagon?

+
The sum of the interior angles of a hexagon is (6-2) × 180° = 720°.
How do you find the measure of an inscribed angle?

+
An inscribed angle is half the measure of the arc it intercepts.
Can the tangent of an angle be greater than 1?

+
Yes, the tangent function can have values greater than 1; it’s only 1 when the angle is 45°.



