5 Mechanical Advantage Problems Solved for You

Mechanical advantage is a fundamental concept in physics and engineering, offering insights into how machines can multiply force, making work easier. Whether you're lifting heavy objects, cutting with scissors, or driving a vehicle, understanding mechanical advantage can significantly enhance efficiency and effectiveness. In this blog post, we'll explore five distinct problems involving mechanical advantage, solving them step-by-step to provide you with practical examples and applications.
1. The Lever and Lifting Weights
A lever is a simple machine where the load, the fulcrum, and the effort are in different positions, creating a mechanical advantage. Consider a scenario where you want to lift a heavy box using a lever.
Problem: You have a 100 kg box you need to lift using a lever. The fulcrum is positioned such that the distance from the fulcrum to the box is 50 cm, and the distance from the fulcrum to the point where you'll apply the force is 300 cm.
- Calculate the mechanical advantage (MA) of the lever.
- Determine the force needed to lift the box.
Solution:
- The formula for the mechanical advantage of a lever is MA =
d1/d2, whered1is the distance from the fulcrum to the effort andd2is the distance from the fulcrum to the load. - Substituting the values: MA = 300 cm / 50 cm = 6.
- To find the force needed, remember that Force needed (F) = Load (L) / Mechanical Advantage (MA). Here, F = (100 kg * 9.81 m/s²) / 6 ≈ 163.5 N.
⚙️ Note: This calculation assumes an ideal machine without friction, which in real-world scenarios could slightly alter the force required.
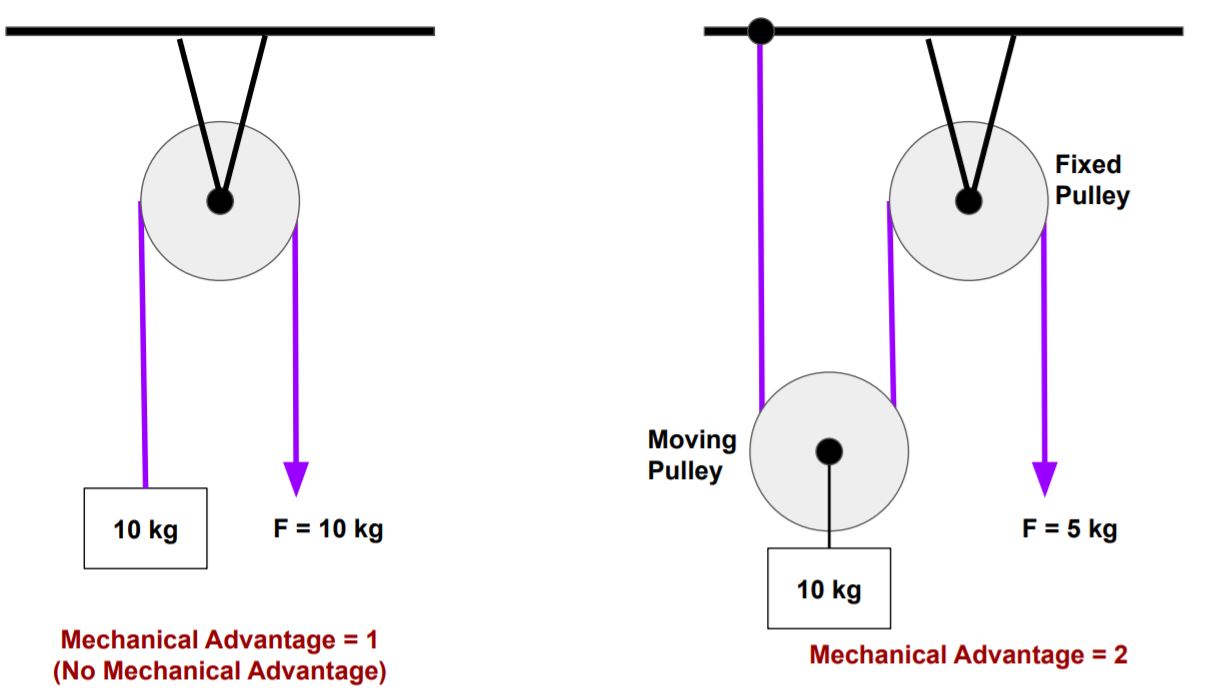
2. The Pulley System

A pulley can change the direction of force and multiply the force applied, providing a mechanical advantage. Imagine you’re using a block and tackle system.
Problem: You have a single movable pulley (a two-pulley system) to lift a 150 kg weight. Calculate the mechanical advantage and the force needed to lift the weight.
Solution:
- The mechanical advantage of a two-pulley system is 2.
- Force needed = Weight / Mechanical Advantage = (150 kg * 9.81 m/s²) / 2 ≈ 735.75 N.
🔧 Note: Each pulley added to the system doubles the mechanical advantage, but it also doubles the length of rope pulled.
3. The Screw and Mechanical Advantage

The screw is a mechanism that converts rotational motion to linear motion, offering a mechanical advantage by transforming a small torque into a large linear force. Consider a jackscrew.
Problem: A jackscrew has threads with a pitch of 5 mm, and you apply a force of 50 N at a lever arm 20 cm long. Calculate the mechanical advantage.
Solution:
- Mechanical Advantage (MA) = 2 * π * r / pitch, where r is the radius of the lever.
- Substituting the values: MA = (2 * π * 0.20 m) / 0.005 m ≈ 251.
💡 Note: This high mechanical advantage makes screw mechanisms incredibly efficient for lifting or clamping, but they require many turns.
4. The Wedge and Mechanical Advantage

A wedge is a simple machine that splits or separates materials. The mechanical advantage depends on its shape.
Problem: You are using a wedge with a slope of 1:3 (1 cm rise over 3 cm run). Find the mechanical advantage.
Solution:
- The mechanical advantage of a wedge = run / rise.
- Substituting the values: MA = 3 cm / 1 cm = 3.
📐 Note: The thinner the wedge, the greater its mechanical advantage, but it also becomes less stable.
5. The Wheel and Axle

The wheel and axle work on the principle of leverage, where a larger wheel is attached to a smaller axle, reducing the effort required to move a load.
Problem: A vehicle's steering wheel has a diameter of 25 cm, while the steering column axle is 5 cm. Calculate the mechanical advantage.
Solution:
- The mechanical advantage = Diameter of wheel / Diameter of axle.
- Substituting the values: MA = 25 cm / 5 cm = 5.
In summary, understanding mechanical advantage helps us appreciate how everyday machines operate to make tasks easier. From the simple lever to complex systems like screw jacks or hydraulic lifts, each machine applies different principles to multiply force or make work more efficient. By exploring these problems, we've seen how mechanical advantage is crucial in various applications, from basic hand tools to sophisticated machinery.
What is mechanical advantage?

+
Mechanical advantage is the ratio of the output force exerted by a machine to the input force applied. It tells you how much a machine multiplies the effort put into it, making work easier or allowing heavier loads to be moved with less force.
Can mechanical advantage be less than one?

+
Yes, mechanical advantage can be less than one if the machine requires more input force than the output it provides. This is often the case with speed multipliers like gears where force is traded for speed.
How does friction affect mechanical advantage?
+
Friction reduces the mechanical advantage of a machine by dissipating some of the input energy as heat or sound. This means that in real-world applications, the actual mechanical advantage will be lower than the theoretical value due to losses caused by friction.



