5 Ways to Master Magnetic Field Calculations
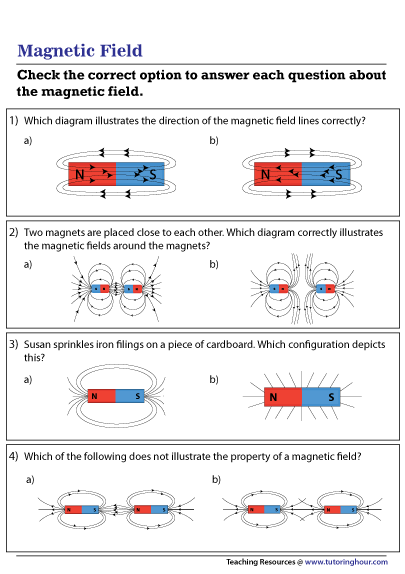
In the intricate world of electromagnetism, mastering magnetic field calculations is paramount for both budding and seasoned electrical engineers. The magnetism in our devices and equipment largely hinges on how accurately and effectively we can calculate and manipulate magnetic fields. This blog post dives into five essential methods to excel at magnetic field calculations, ensuring your designs are both optimized and efficient.
Understanding the Basics of Magnetic Fields

Before delving into complex calculations, it's crucial to have a solid grounding in the principles governing magnetic fields. Here's a brief overview:
- Magnetic Field (B): The vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials.
- Magnetic Flux Density: Measured in Tesla (T), it indicates how dense the magnetic field lines are in a region.
- Permeability: Describes how easily a magnetic field can be established within a material. The permeability of free space (μ₀) is 4π × 10-7 H/m.
- Biot-Savart Law: Used to calculate the magnetic field generated by an electric current.
Method 1: Biot-Savart Law

The Biot-Savart law is fundamental when calculating the magnetic field due to a current-carrying conductor:
Formula:

[ B = \frac{\mu_0}{4\pi} \int \frac{Id \mathbf{l} \times \mathbf{r}}{|\mathbf{r}|^3} ]
Where:
- B: Magnetic field at a point.
- I: Current flowing through the conductor.
- dl: Differential element of length along the conductor.
- r: Vector from the current element to the point in space.
To apply this law:
- Identify the differential current element (d).
- Determine the vector from dl to the point where the magnetic field is to be calculated (r).
- Calculate the cross product dl × r.
- Divide the result by |r|³.
- Integrate this expression over the entire current path.
💡 Note: When calculating magnetic fields, always ensure consistent unit usage to avoid errors in the calculation.
Method 2: Ampere's Law

Ampere's Law relates magnetic fields to electric currents using a simpler integral form:
Formula:
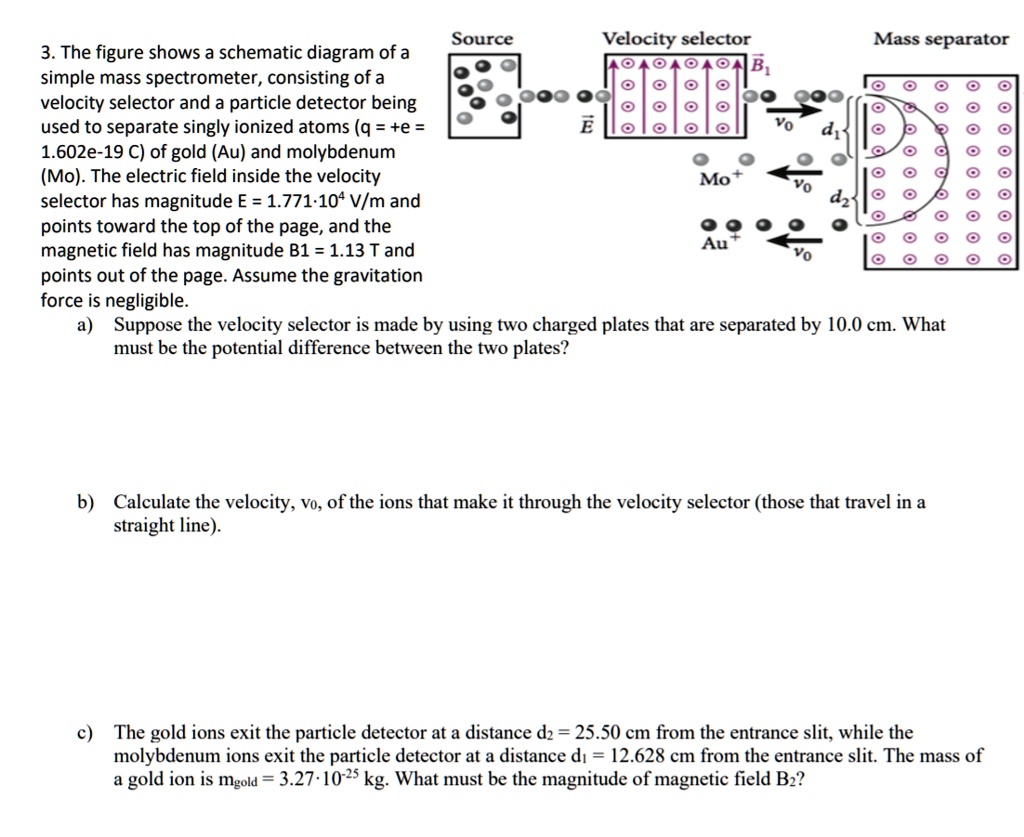
[ \oint B \cdot d\mathbf{l} = \mu0 I{enc} ]
Where:
- B: Magnetic field.
- dl: Differential line element.
- μ₀: Permeability of free space.
- I_enc: Current enclosed by the loop.
Steps to apply Ampere's Law:
- Choose a closed loop (Amperian loop).
- Calculate the dot product B · dl along the loop.
- Sum this product to find the total circulation.
- Set this equal to μ₀I_enc, where I_enc is the current passing through the loop.
Method 3: Using Finite Element Analysis (FEA)

Finite Element Analysis provides a numerical approach to calculating magnetic fields in complex geometries:
- Divide the region of interest into small, finite elements.
- Define the material properties for each element.
- Apply boundary conditions.
- Use software to solve Maxwell's equations within these elements.
- Post-process the results to visualize magnetic fields.
📝 Note: FEA can be computationally intensive but offers high precision for complex structures.
Method 4: Magnetic Scalar Potential Method

This method simplifies field calculations in regions where no current flows:
- Define the magnetic scalar potential (φm) where ∇²φm = 0.
- Calculate φm using boundary conditions.
- Obtain the magnetic field through the gradient: B = -μ₀∇φm.
Method 5: Analogous Electric Field Techniques

By utilizing the duality between electric and magnetic fields, one can solve magnetic field problems using electric field solutions:
- Transform the magnetic problem into an equivalent electric problem using substitution.
- Use known electric field techniques like Poisson’s or Laplace’s equations.
- Reinterpret the electric field results back into magnetic terms.
This synthesis of various calculation methods not only enhances understanding but also provides engineers with the tools needed to design systems that efficiently leverage electromagnetic principles.
As we've seen, mastering magnetic field calculations involves understanding both the theoretical underpinnings and practical applications of these fields. Each method provides unique insights and approaches to tackle different types of problems:
- The Biot-Savart Law and Ampere's Law give you an analytical framework.
- Finite Element Analysis offers numerical precision for complex structures.
- Magnetic Scalar Potential simplifies calculations in current-free regions.
- Analogous electric field techniques provide an innovative way to understand magnetic fields.
By embracing these methods and combining them with practical experience, engineers can enhance their ability to design and analyze electromagnetic devices, ensuring better performance and innovation in their fields.
How does the Biot-Savart Law differ from Ampere’s Law?

+
The Biot-Savart Law calculates the magnetic field at a point due to a current-carrying conductor. It integrates the contributions from all current elements. In contrast, Ampere’s Law uses a circulation integral to relate the magnetic field around a closed loop to the total current passing through that loop. Essentially, Biot-Savart is more suited for point calculations, while Ampere’s Law is useful for symmetrical configurations.
When should I use Finite Element Analysis?

+
FEA is ideal when dealing with complex geometries, non-uniform material properties, or when accurate field distribution is crucial. It’s particularly beneficial when analytical methods become impractical or when you need to analyze field behavior under varying conditions or with intricate boundary conditions.
Can magnetic fields be calculated with just an understanding of electricity?

+
Yes, by leveraging the duality between electric and magnetic fields. This method involves transforming magnetic field problems into equivalent electric field problems using known solutions from electrostatics, then translating the results back to magnetism.



