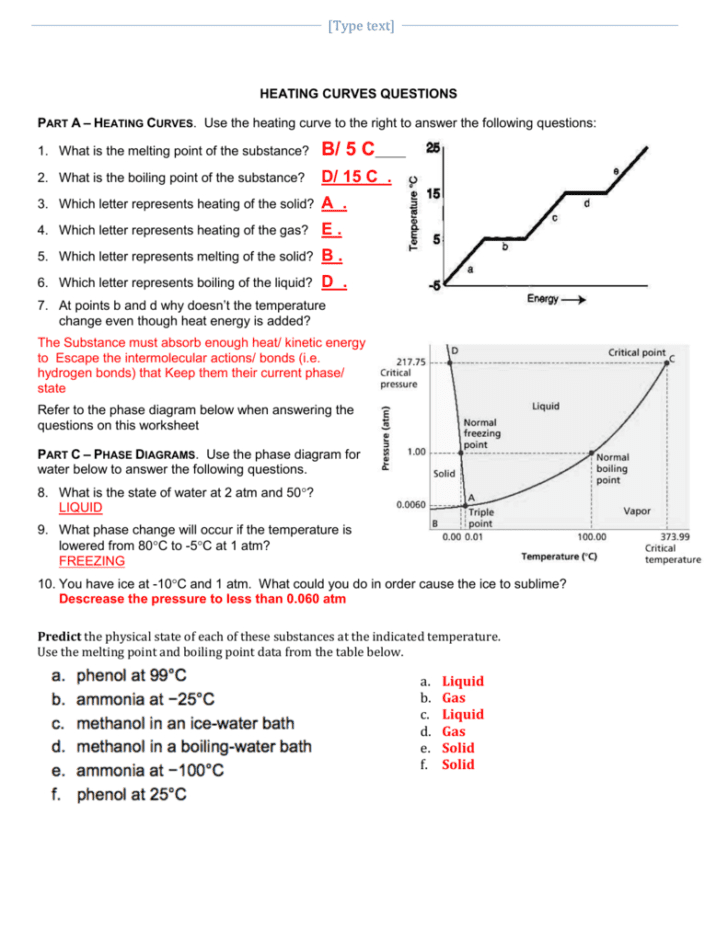
Master Long Division with No Remainder Practice Sheets

Mastering long division can be a daunting task for many students, but it doesn't have to be. With the right approach and practice, long division can become an intuitive and straightforward process. This blog post will guide you through the essentials of long division with no remainder, providing you with practice sheets and tips to ensure proficiency in this fundamental arithmetic operation.
What is Long Division?

Long division is a method used to divide large numbers by another number, particularly when the divisor is a two-digit or larger number. Unlike short division, long division allows you to break down the process into manageable steps, making complex calculations more approachable.
- Dividend: The number being divided.
- Divisor: The number by which we are dividing.
- Quotient: The result of the division.
- Remainder: The number left over after division if the dividend does not divide evenly by the divisor.
Steps for Long Division with No Remainder

Here are the steps to perform long division where you aim for a quotient with no remainder:
- Set Up: Write the dividend under a division bracket and the divisor to its left.
- Divide: Determine how many times the divisor goes into the first digit (or digits) of the dividend. This number goes above the line.
- Multiply: Multiply the number above the line by the divisor and write the product under the selected part of the dividend.
- Subtract: Subtract this product from the part of the dividend you've used. Bring down the next digit of the dividend to continue the process.
- Repeat: Repeat steps 2 through 4 until you've used all digits of the dividend. If at the end, there's no remainder, you've successfully divided with no remainder.
Practice Sheets for Long Division

Practice is key to mastering long division. Here are some practice sheets designed to help you:
Basic Level

- Divide 3-digit numbers by 1-digit numbers
- Example: 369 ÷ 3
Intermediate Level
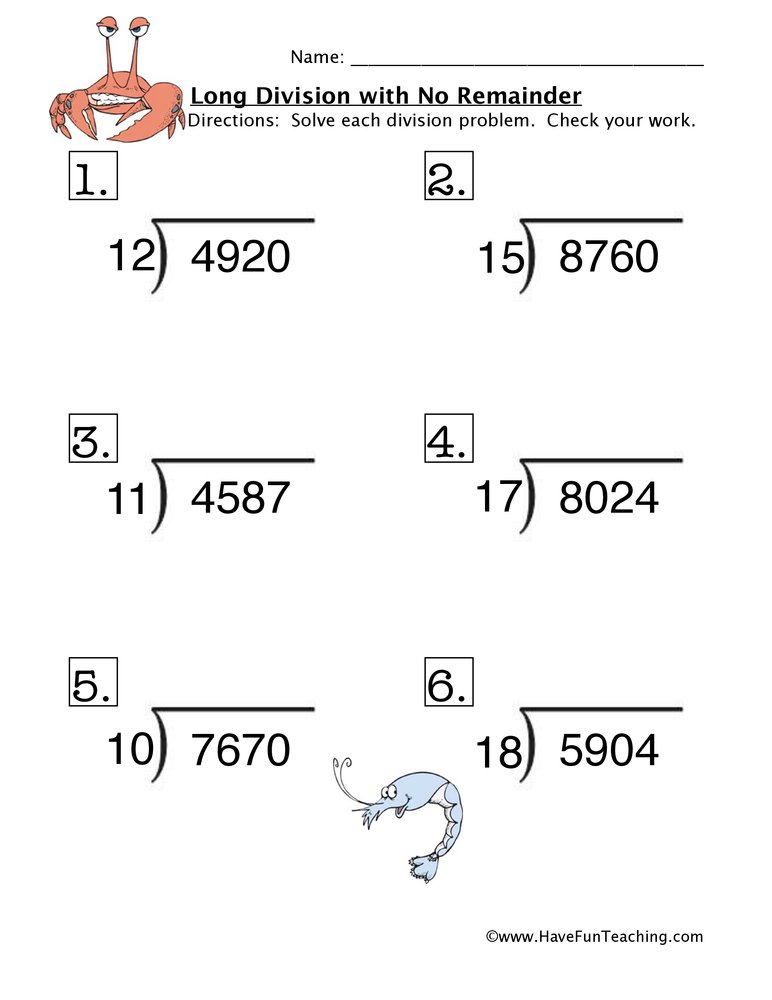
- Divide 3-digit or 4-digit numbers by 2-digit numbers
- Example: 1288 ÷ 16
Advanced Level

- Dividing large numbers with more complex divisors
- Example: 7242 ÷ 26
Strategies for Tackling Long Division

Here are some strategies to improve your long division skills:
- Estimation: Estimate how many times the divisor fits into the dividend to get an idea of the quotient quickly.
- Learn Patterns: Familiarize yourself with common division patterns, like the ones involving multiples of 11 or 9.
- Use Visuals: Drawing out the problem can help visual learners see the division steps clearly.
- Chunking: For larger numbers, break down the dividend into manageable chunks before dividing.
🔍 Note: Practicing division regularly will enhance your speed and accuracy, making the process less intimidating over time.
Table of Common Long Division Scenarios

| Dividend | Divisor | Steps |
|---|---|---|
| 182 | 2 | 18 ÷ 2 = 9, 2 goes into 182 twice (91 × 2), subtract to get 0. |
| 1562 | 3 | 3 goes into 15 five times (15 ÷ 3 = 5), 3 goes into 62 twice (6 ÷ 3 = 2), remaining 0. |
| 3024 | 12 | 12 goes into 30 twice (30 ÷ 12 = 2.5, but since we need whole numbers, 2), 12 goes into 62 five times (62 ÷ 12 = 5.16, but rounding gives 5), remaining 0. |

The above scenarios provide practical examples of long division that result in no remainder, illustrating the process step by step.
Mastering Long Division: A Summary
By understanding the fundamental steps of long division and practicing with diverse examples, students can become proficient in this arithmetic operation. Long division, once feared, can become an intuitive process through consistent practice and the application of strategic approaches. Remember to:
- Practice regularly
- Use estimation to set expectations
- Break down the problem into manageable parts
- Learn and apply division patterns
Why is it important to learn long division?

+
Long division teaches problem-solving, logical thinking, and a deeper understanding of numerical operations, which are essential for advanced mathematics and real-world applications like budgeting or understanding stock prices.
What should I do if my child struggles with long division?

+
Start with simple problems and gradually increase difficulty, use visuals or physical objects to represent division, and consider using practice sheets tailored to their level. Encouraging them to think aloud or explain the process can also reveal where they might be getting confused.
Are there any tips for dividing when the remainder is significant?

+
If the remainder is significant, you can round up or down the quotient depending on the context. For precision, you can also convert the remainder into a decimal or continue the division process to get the fractional part of the quotient.