Mastering Long Division with 2-Digit Divisors: Free Worksheet

The journey of mastering long division with 2-digit divisors can initially seem daunting, but with the right guidance and practice, it becomes an accessible skill for students at various educational levels. Understanding the mechanics behind dividing by larger numbers not only strengthens one's arithmetic abilities but also lays a solid foundation for more advanced math concepts. Here, we delve into the nuances of long division, offering a step-by-step guide complemented by a free worksheet to help solidify this essential mathematical technique.
Understanding Long Division Basics

Long division is a method used to divide one number by another when the divisor (the number doing the dividing) is greater than nine. Here’s a basic outline:
- Dividend: The number being divided.
- Divisor: The number you're dividing by.
- Quotient: The result of the division.
- Remainder: The leftover after division, if any.
Steps to Master Long Division with 2-Digit Divisors

Step 1: Set Up the Problem

Begin by writing the problem in the correct format:
- Write the dividend inside a bracket or a long division symbol.
- The divisor goes outside the bracket.
📝 Note: Ensure the alignment of numbers in the problem setup as it can help prevent errors in calculation.
Step 2: Divide the First Two Digits
If the first digit of the dividend is smaller than the divisor, consider the first two digits for division. This ensures you have a workable number to start with:
- If the first digit is larger, divide by the divisor. Write the result at the top of the division bracket.
- If the result is a two-digit number, subtract only the last digit from the first digit of the dividend.
- Continue this process with the next digit of the dividend, bringing it down beside the result.
| Dividend | Divisor |
| 345 | 12 |

In this example, 12 cannot divide into 3, so we consider 34 (which can be divided by 12). 12 goes into 34 exactly two times, so we write 2 above the division bar.
Step 3: Multiply and Subtract

Multiply the divisor by this partial quotient (2) and write the result below the digits you just divided. Subtract this from the digits above:
- 12 multiplied by 2 equals 24.
- Subtract 24 from 34 to get 10. Write 10 below the 34.
Step 4: Bring Down and Repeat
Bring down the next digit (5 in our case) to the right of the remainder (10). This creates a new number to divide:
- Bring down the 5, making it 105.
- 12 goes into 105 eight times (since 12 multiplied by 8 is 96, which is less than or equal to 105).
- Write 8 next to the 2 above the division bar.
Step 5: Repeat the Process

Repeat steps 3 and 4 until you have used all the digits in the dividend, or until the remainder is less than the divisor:
- Subtract 96 from 105 to get a remainder of 9.
- If there are more digits, continue dividing, multiplying, and subtracting; otherwise, stop if the remainder is smaller than the divisor.
⚠️ Note: If at any step you cannot divide, check your setup again. Common errors include misalignment or incorrect division.
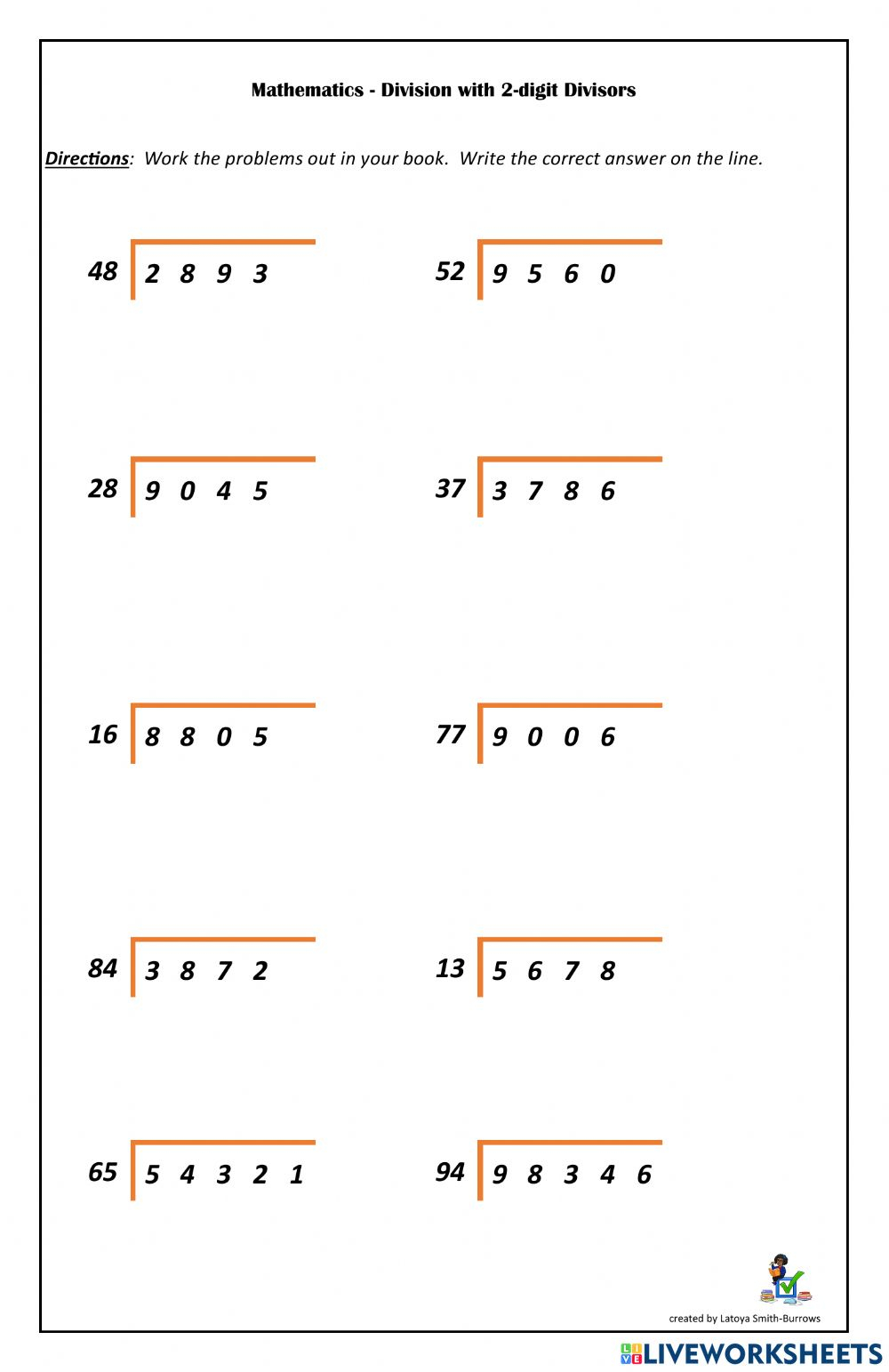
Practice with a Free Worksheet

To put these steps into practice, here is a simple worksheet designed to help students refine their long division skills:
Download this worksheet for more problems.
In summary, mastering long division with 2-digit divisors involves understanding the concept of carrying down digits, continuously dividing, and ensuring that remainders are appropriately managed. This skill not only enhances mathematical proficiency but also prepares students for more complex arithmetic and algebra. Through practice, students can build confidence in tackling these problems, thereby setting the stage for future success in math.
Why is long division important?

+
Long division is crucial for understanding the division process deeply, which is foundational for algebra, handling proportions, and dealing with more complex mathematical problems in later education.
What do I do if the remainder is larger than the divisor?

+
If the remainder is larger than the divisor, you need to revise your division step. Either the quotient is incorrect, or you’ve made an error in the multiplication or subtraction steps.
Can long division be used for fractions?

+
Yes, long division can also be applied to calculate the decimal expansion of fractions by continually dividing until you achieve the desired precision or a repeating decimal pattern.



