5 Ways to Solve Linear Equations Easily

Understanding Linear Equations

Linear equations are a fundamental concept in mathematics, and solving them is a crucial skill for students, professionals, and anyone who wants to improve their problem-solving abilities. A linear equation is an equation in which the highest power of the variable(s) is 1. It can be written in the form of ax + b = 0, where ‘a’ and ‘b’ are constants, and ‘x’ is the variable. In this article, we will explore five ways to solve linear equations easily.
Method 1: Addition and Subtraction

One of the simplest ways to solve linear equations is by using addition and subtraction. This method involves isolating the variable by adding or subtracting the same value to both sides of the equation.
For example, consider the equation: 2x + 5 = 11
To solve for x, subtract 5 from both sides:
2x + 5 - 5 = 11 - 5 2x = 6
Next, divide both sides by 2:
2x / 2 = 6 / 2 x = 3
Therefore, the value of x is 3.
📝 Note: When using addition and subtraction to solve linear equations, make sure to perform the same operation on both sides of the equation to maintain equality.
Method 2: Multiplication and Division

Another way to solve linear equations is by using multiplication and division. This method involves isolating the variable by multiplying or dividing both sides of the equation by the same value.
For example, consider the equation: 4x = 24
To solve for x, divide both sides by 4:
4x / 4 = 24 / 4 x = 6
Therefore, the value of x is 6.
📝 Note: When using multiplication and division to solve linear equations, make sure to perform the same operation on both sides of the equation to maintain equality.
Method 3: Cross-Multiplication

Cross-multiplication is a method used to solve linear equations in the form of ax/b = c/d. This method involves multiplying both sides of the equation by the denominators to eliminate the fractions.
For example, consider the equation: 2x/3 = 4⁄5
To solve for x, cross-multiply:
2x × 5 = 4 × 3 10x = 12
Next, divide both sides by 10:
10x / 10 = 12 / 10 x = 6⁄5
Therefore, the value of x is 6⁄5.
Method 4: Using Inverse Operations

Inverse operations are pairs of operations that undo each other. For example, addition and subtraction are inverse operations, and multiplication and division are inverse operations. Using inverse operations can help solve linear equations.
For example, consider the equation: x + 2 = 7
To solve for x, use the inverse operation of addition, which is subtraction:
x + 2 - 2 = 7 - 2 x = 5
Therefore, the value of x is 5.
Method 5: Using Online Tools and Resources

In today’s digital age, there are many online tools and resources available to help solve linear equations. These tools can range from simple calculators to advanced computer algebra systems.
For example, consider the equation: 3x - 2 = 11
To solve for x, use an online calculator or computer algebra system:
3x - 2 = 11 3x = 11 + 2 3x = 13 x = 13⁄3 x = 4.33
Therefore, the value of x is approximately 4.33.
Now that we have explored five ways to solve linear equations easily, it’s time to summarize the key points.
In summary, solving linear equations is a fundamental skill that can be achieved using various methods. Whether you use addition and subtraction, multiplication and division, cross-multiplication, inverse operations, or online tools and resources, the key is to isolate the variable and maintain equality. By mastering these methods, you’ll become proficient in solving linear equations and be better equipped to tackle more complex mathematical problems.
What is a linear equation?

+
A linear equation is an equation in which the highest power of the variable(s) is 1. It can be written in the form of ax + b = 0, where ‘a’ and ‘b’ are constants, and ‘x’ is the variable.
What are the different methods to solve linear equations?

+
There are several methods to solve linear equations, including addition and subtraction, multiplication and division, cross-multiplication, using inverse operations, and using online tools and resources.
How do I know which method to use to solve a linear equation?
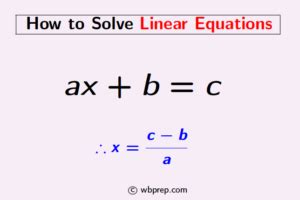
+
The method to use depends on the form of the equation and the values of the constants. For example, if the equation is in the form of ax = b, you can use multiplication and division. If the equation is in the form of ax/b = c/d, you can use cross-multiplication.
Related Terms:
- Solving Linear Equations Worksheet PDF
- solving single variable equations worksheet
- linear equation worksheet with answer
- linear equation exercise pdf
- linear equations worksheet answer key
- one variable equations worksheet pdf