Mastering Exponents: Free Laws Worksheet with Answers

Understanding exponents is a fundamental aspect of mathematics that can significantly enhance one's ability to deal with larger or more complex numbers efficiently. Exponents, or powers, are a shorthand method for expressing repeated multiplication of the same number. Today, we're diving into the Laws of Exponents to clarify these rules and provide you with a free worksheet to help solidify your understanding.
Why Exponents Matter

Exponents appear in various forms in algebra, calculus, scientific notation, and even in real-life scenarios like calculating compound interest. Here's why they are important:
- Simplification: Exponents allow for the quick computation of large numbers.
- Pattern Recognition: They help in identifying mathematical patterns and relationships.
- Time Efficiency: Using exponents reduces the time spent on repetitive calculations.
The Laws of Exponents

Here are the fundamental laws of exponents that everyone should know:
1. Product Rule

The product rule states that when multiplying two exponents with the same base, you add their exponents:
am × an = am+n
2. Quotient Rule

The quotient rule applies when dividing two exponents with the same base; here, you subtract the exponent in the denominator from the one in the numerator:
am ÷ an = am-n
3. Power Rule

The power rule is used when an exponent is raised to another exponent. You multiply the exponents:
(am)n = am×n
4. Zero Exponent Rule
Any non-zero number raised to the power of zero equals one:
a0 = 1
🚨 Note: Zero raised to any power is still zero, but any number (except zero) raised to the power of zero is always one.
5. Negative Exponent Rule

A negative exponent indicates that the base is to be raised to the positive exponent and then inverted:
a-m = 1/am
6. Fractional Exponents

A fractional exponent can be interpreted as the root (or power) of the base:
am/n = (√a)m
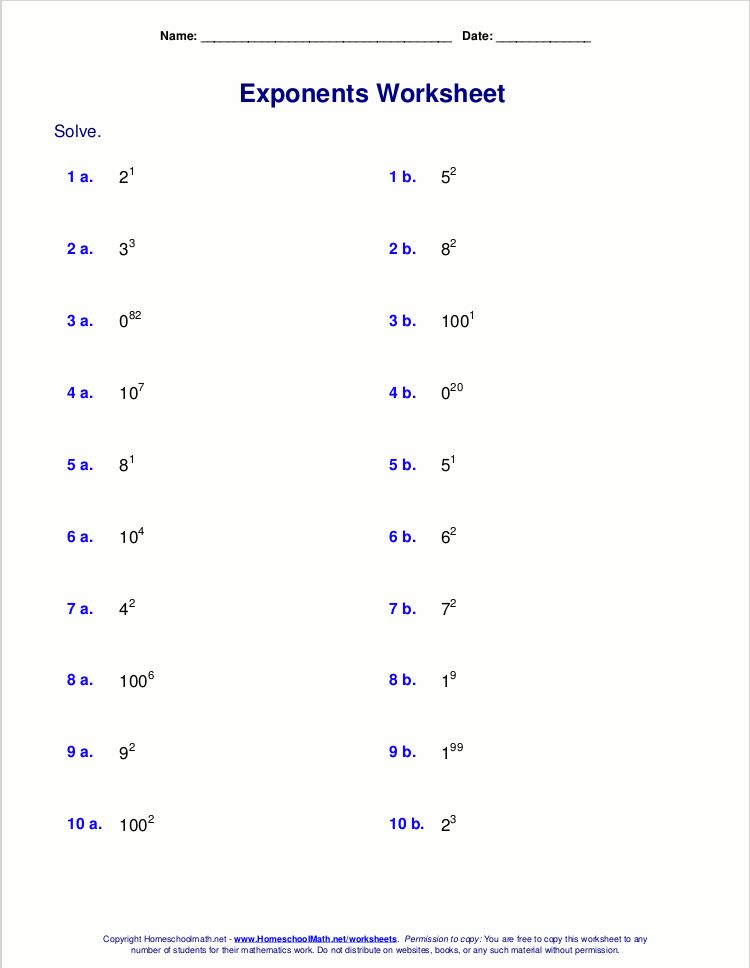
Free Laws of Exponents Worksheet

To help you master these laws, here is a concise worksheet with problems and answers:
| Problem | Answer |
|---|---|
| 52 × 54 | 56 |
| (35) / (33) | 32 |
| (23)2 | 26 |
| 90 | 1 |
| 4-2 | 1/42 = 1/16 |
| 161/2 | 4 (since 42 = 16) |

Practical Application of Exponents

Exponents are not just theoretical; they're incredibly practical:
- Scientific Notation: Used to express very large or very small numbers, making them easier to work with.
- Population Growth: Understanding how populations or values grow over time can be modeled using exponential growth equations.
- Computer Science: Algorithms and data structures often involve operations that can be described with exponents.
📝 Note: While this post covers basic laws, there are more advanced exponent rules for more complex algebraic expressions.
Conclusion Paragraph

The laws of exponents are crucial for simplifying and solving mathematical expressions involving powers. By mastering these rules, you can quickly handle large numbers, recognize patterns, and streamline calculations. The free worksheet provided here gives you a practical tool to test your understanding of these laws. Remember, practice is key to becoming proficient in any mathematical concept. Embrace the power of exponents to unlock new levels of mathematical prowess and see where it takes you in your journey through mathematics.
What is the purpose of using exponents in math?

+
Exponents are used to simplify repeated multiplication and to denote powers in mathematical expressions, making it easier to work with large or small numbers, as well as understand growth or decay patterns.
Can you explain why any number raised to zero is one?

+
In the context of exponents, any number raised to the power of zero reflects the identity property of multiplication; essentially, any number multiplied by one remains unchanged, and when we consider a0, we’re essentially multiplying an by a0-n which equals one because any number divided by itself is one.
How can I remember the laws of exponents?

+
One way to remember these laws is by understanding them conceptually rather than just memorizing them. However, mnemonic devices like acronyms or visual aids can also help. For instance, think of P for Power (multiply exponents when raising to a power), Q for Quotient (subtract exponents when dividing), and so on.