5 Essential Tips for Mastering Law of Exponents

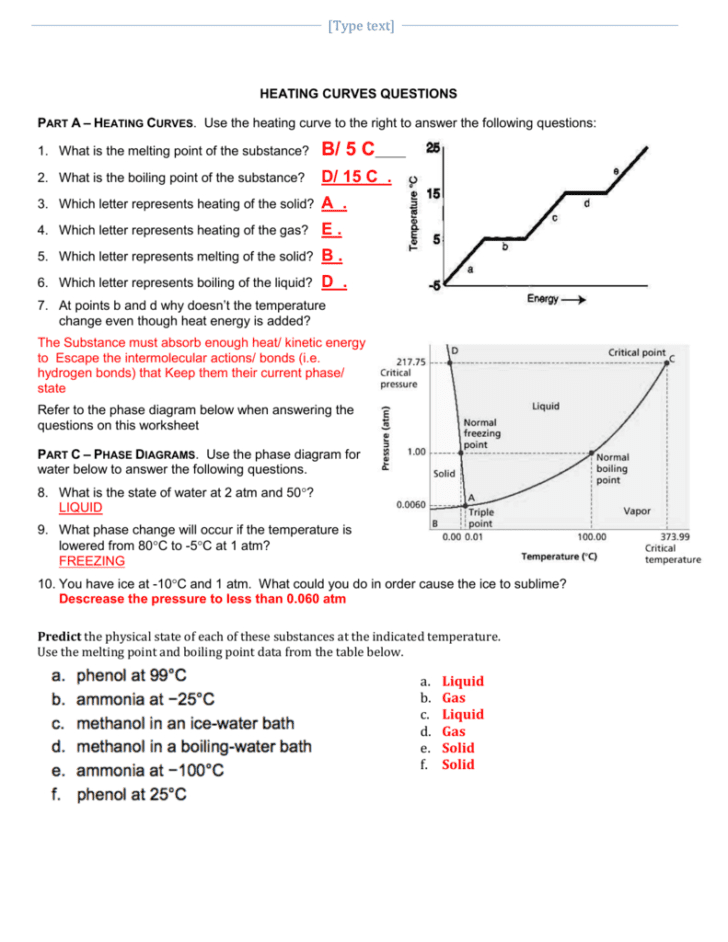
The law of exponents, often referred to as the rules of exponents, is a fundamental concept in algebra and mathematics. These laws provide the framework for manipulating expressions with exponents, making it easier to simplify, evaluate, and solve various mathematical problems. Understanding these rules is critical not only for academic pursuits but also for practical applications in fields like science, engineering, and finance. Here, we will delve into five essential tips for mastering the law of exponents that can make complex calculations more manageable.
1. Understand the Basic Rules

The foundation of mastering the law of exponents lies in understanding the basic rules:
- Product of Powers: (a^m \cdot a^n = a^{m+n}) - When multiplying two exponents with the same base, add the exponents.
- Quotient of Powers: (\frac{a^m}{a^n} = a^{m-n}) - When dividing two exponents with the same base, subtract the exponents.
- Power of a Product: ((a \cdot b)^n = a^n \cdot b^n) - When a product is raised to an exponent, distribute the exponent to each factor.
- Power of a Quotient: (\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}) - Similar to the product, when a fraction is raised to an exponent, apply the exponent to the numerator and the denominator separately.
- Power of a Power: ((a^m)^n = a^{m \cdot n}) - When an exponent is raised to another exponent, multiply the exponents.
- Zero Exponent: (a^0 = 1) - Any nonzero number raised to the power of zero is 1.
- Negative Exponents: (a^{-n} = \frac{1}{a^n}) - Any nonzero number raised to a negative exponent is equivalent to its reciprocal with a positive exponent.
💡 Note: Understanding these rules is not just about memorization but applying them to solve complex problems effectively.
2. Practice Simplifying Expressions


The more you practice simplifying expressions, the better you will become at instinctively applying these rules:
- Start with simple expressions like (4^2 \cdot 4^3) or (\left(\frac{2}{3}\right)^4).
- Move on to more complex ones such as (a^3 \cdot a^{-4}) or (\left(\frac{a}{b}\right)^2 \cdot \left(\frac{b}{c}\right)^3).
- Use online resources or textbooks to find exercises tailored to your skill level.
3. Use Visual Aids and Mnemonics

To help remember the rules:
- Create visual aids like charts or flashcards where each rule is summarized with examples.
- Develop mnemonics. For example:
- Product of Powers: “Add ‘em up” - you add the exponents.
- Quotient of Powers: “Subtract ‘em” - you subtract the exponents.
🎨 Note: Visual aids can significantly enhance memory retention for abstract mathematical concepts.
4. Apply Exponents in Real-Life Scenarios

Understanding how exponents work in real-world contexts can solidify your grasp:
- Compound Interest: Use exponents in calculating how investments grow over time.
- Scientific Notation: Astronomers, scientists, and engineers often use exponents to represent very large or small numbers.
- Population Growth: Model exponential growth in biology or economics.
📈 Note: Applying exponents to real-life scenarios makes the concept not only tangible but also underscores its importance.
5. Master Negative and Fractional Exponents

Once the basic rules are in place, delve into more complex scenarios:
- Negative Exponents: Understand that (a^{-n}) is the same as (\frac{1}{a^n}). Practice converting between negative exponents and their positive equivalents.
- Fractional Exponents: Learn that (a^{m/n} = \sqrt[n]{a^m}) or (a^{1/n} = \sqrt[n]{a}). Recognize that roots and exponents are interconnected.
Summary

In mastering the law of exponents, you not only enhance your algebraic skills but also gain a deeper understanding of how mathematics applies to the world around us. These five tips, from understanding the basic rules to applying exponents in real-life scenarios, provide a comprehensive strategy for anyone looking to excel in this critical area of math. The journey involves practice, visual aids, real-world applications, and embracing the complexities like negative and fractional exponents, ensuring a thorough understanding that transcends mere academic requirements.
What are the most common mistakes when applying the law of exponents?

+
The most common mistakes include: misunderstanding the difference between adding and multiplying exponents, ignoring the base, and forgetting the zero-exponent rule.
How can I tell if I’ve mastered the law of exponents?

+
You’ve likely mastered the law of exponents if you can instinctively apply all the rules without confusion, solve complex problems quickly, and teach or explain these concepts to others with ease.
Why are exponents important in mathematics?

+
Exponents simplify complex calculations, allow for easier modeling of growth, decay, and power functions, and are fundamental in fields like calculus, finance, physics, and engineering.