5 Kinematic Equations You Must Know With Answers
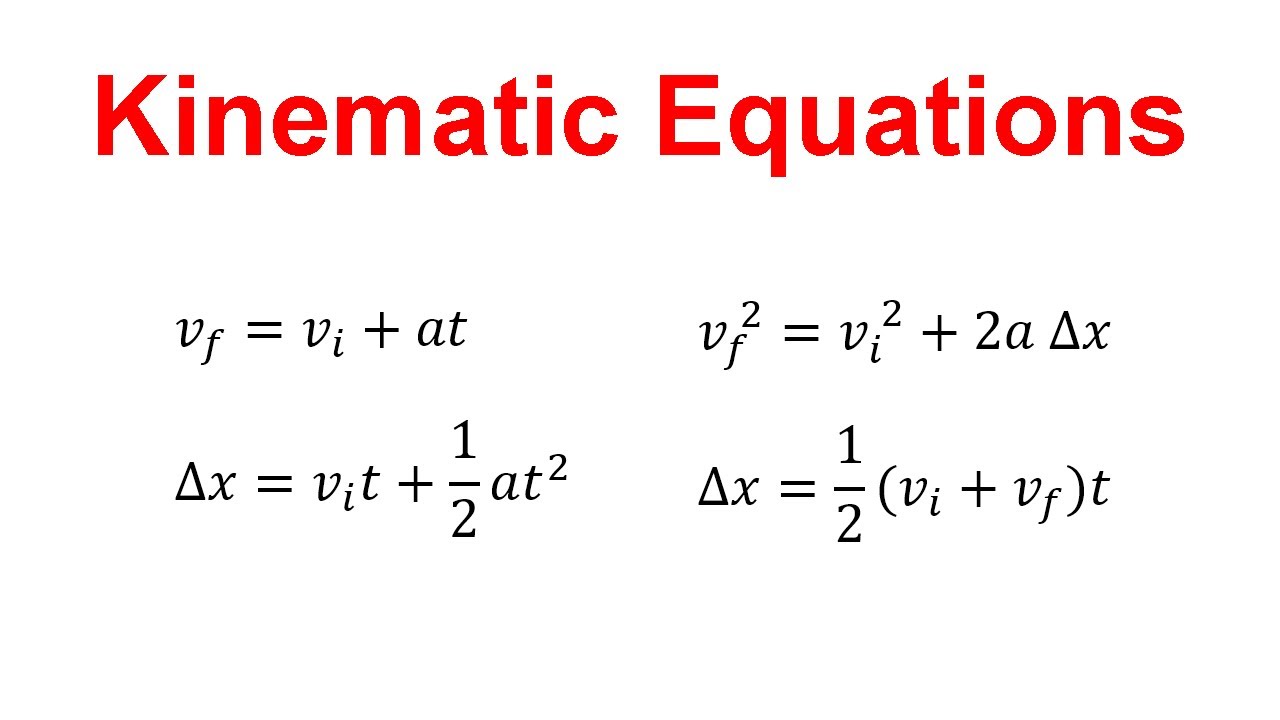
Understanding kinematic equations is crucial for anyone studying physics, whether you're a high school student preparing for exams or a curious mind delving into the mechanics of motion. Kinematics, the branch of classical mechanics, deals with the motion of objects without considering the forces that cause this motion. Here, we will explore five essential kinematic equations, providing a comprehensive understanding of how to use them along with examples and explanations.
1. The Definition of Kinematic Equations

Kinematic equations allow us to describe the motion of objects. These equations are derived from the basic definitions of velocity, acceleration, displacement, and time. Here’s how they look:
| Equation | Description |
|---|---|
| v = u + at | Velocity as a function of initial velocity, acceleration, and time. |
| s = ut + 0.5at2 | Displacement considering initial velocity, acceleration, and time squared. |
| v2 = u2 + 2as | Final velocity squared in terms of initial velocity, acceleration, and displacement. |
| s = (u + v)/2 * t | Displacement using average velocity and time. |
| a = (v - u)/t | Acceleration as a function of velocity change and time. |

⚠️ Note: In these equations, s is displacement, u is initial velocity, v is final velocity, a is acceleration, and t is time.
2. Solving Kinematic Problems

To solve kinematic problems, you need to identify which kinematic equation to use based on the given information and what you need to solve for. Here’s how to approach it:
- Identify the knowns: What variables do you know?
- Determine the unknown: What variable are you solving for?
- Choose the equation: Select the equation that has all the knowns and the unknown variable.
Let's look at an example:
Example Problem:

A car accelerates uniformly from 10 m/s to 30 m/s over 20 seconds. What is its acceleration, and how far does it travel in this time?
- Identify knowns: u = 10 m/s, v = 30 m/s, t = 20 s
- Unknowns: a (acceleration) and s (displacement)
- To find acceleration:
- Use the equation a = (v - u)/t
- a = (30 m/s - 10 m/s) / 20 s = 1 m/s2
- To find displacement:
- Use the equation s = ut + 0.5at2
- s = (10 m/s * 20 s) + 0.5 * (1 m/s2) * (20 s)2 = 600 m
✅ Note: Ensure that the units are consistent throughout the calculation.
3. When to Use Each Kinematic Equation

Each kinematic equation serves a different purpose:
- When you know initial and final velocities, time, and acceleration, use v = u + at.
- To find displacement with acceleration and time, use s = ut + 0.5at2.
- If displacement and acceleration are known but time isn’t, use v2 = u2 + 2as.
- For average velocity to find displacement, use s = (u + v)/2 * t.
- When you need acceleration, use a = (v - u)/t.
4. Graphical Representation of Motion

Graphically, kinematic equations can be visualized through distance-time and velocity-time graphs, which provide an intuitive understanding of how an object moves:
Distance-Time Graph:

This graph shows how the position of an object changes over time. The slope of this graph at any point represents the velocity.
Velocity-Time Graph:

This graph illustrates how velocity changes over time. The slope here represents acceleration, and the area under the curve gives displacement.
5. Limitations and Assumptions of Kinematic Equations

Kinematic equations work under specific assumptions:
- Uniform acceleration or deceleration, meaning acceleration is constant.
- Motion in one dimension (linear motion).
- Time interval starts at zero.
- Ignoring effects like air resistance or friction.
These assumptions simplify the equations but limit their application in real-world scenarios where such conditions are rarely met.
💡 Note: In complex scenarios, you might need to use calculus to describe motion accurately.
To wrap up, understanding the five kinematic equations provides a foundation for solving problems related to motion. They help in calculating distances, velocities, accelerations, and time for objects moving in a straight line with constant acceleration. By applying these equations, we gain insights into how objects move, how fast they go, and how quickly their speed changes. Remember that while these equations offer a simplified view, real-world applications might require adjustments for additional forces and non-uniform conditions. Knowledge of these equations also sets the stage for diving deeper into dynamics, where forces and energy come into play. This foundational knowledge in kinematics opens up many avenues for further exploration in physics, from mechanics to engineering, and even into the realms of space exploration.
What are the kinematic equations?

+
The kinematic equations are a set of formulas used in physics to describe the motion of objects with constant acceleration. These include v = u + at, s = ut + 0.5at^2, v^2 = u^2 + 2as, s = (u + v)/2 * t, and a = (v - u)/t.
How do you use the kinematic equations?

+
To use kinematic equations, identify the known variables (u, v, a, t, s) and use the equation that does not include the variable you need to solve for.
Can these equations be used for three-dimensional motion?

+
No, these equations assume motion in one dimension. For three-dimensional motion, vector calculus or the three-dimensional extension of these equations is needed.



