5 Tips for Isosceles Triangle Worksheet Answers

Exploring and solving exercises on isosceles triangles can significantly enhance one's understanding of geometry, particularly the symmetrical beauty these shapes possess. In this guide, we'll delve into five essential tips that can help you master worksheet answers on isosceles triangles, ensuring your success in geometry classes or self-study.
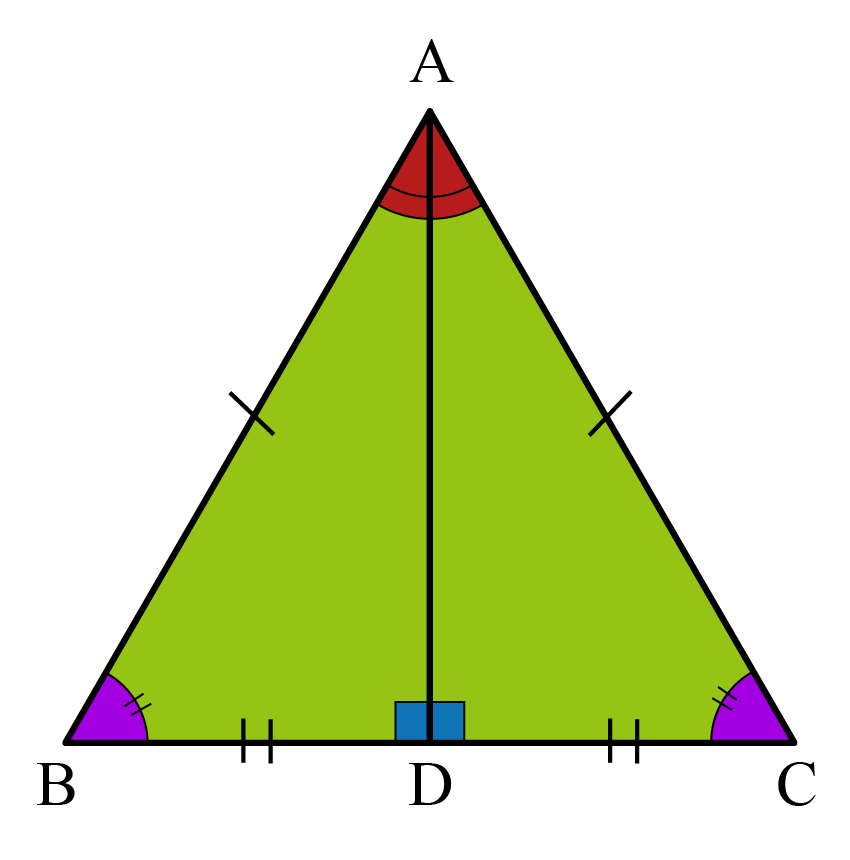
Understanding the Basics of Isosceles Triangles

An isosceles triangle is defined by having at least two sides of equal length, which inherently leads to:
- Equal angles opposite the congruent sides.
- The base angles are always congruent.
- The line of symmetry bisecting the base and the angle at the vertex.

🔍 Note: Being able to identify and label the parts of an isosceles triangle correctly is fundamental to solving geometric problems.
Tip 1: Utilize the Isosceles Triangle Theorem

The theorem states that if two sides of a triangle are congruent, then the angles opposite those sides are also congruent. Here’s how to apply it:
- When given two congruent sides, assume the corresponding angles are also equal.
- If one angle of the isosceles triangle is known, you can deduce the other base angle by subtracting the known angle from 180° and dividing by 2.
Example: Given an isosceles triangle ABC with AB = AC and the vertex angle ∠A = 40°, the base angles ∠B and ∠C are:
- (180° - 40°) / 2 = 70°
💡 Note: Always verify your calculations against the triangle sum theorem (the sum of angles in a triangle equals 180°).
Tip 2: Know the Isosceles Triangle Properties

Here’s a handy table summarizing key properties of isosceles triangles:
| Property | Description |
|---|---|
| Angle Bisector | The line from the vertex to the midpoint of the base bisects the angle at the vertex. |
| Median | Coincides with the altitude, which also serves as the angle bisector and line of symmetry. |
| Perimeter | The sum of all sides, with the equal sides playing a significant role. |
| Area | (Base * Height) / 2, where height is from vertex to the base’s midpoint. |

Tip 3: Use Geometric Constructions

When constructing or solving for an isosceles triangle, remember these steps:
- Start with a line segment (base), then choose a point above this segment to ensure equal sides.
- Use a compass to draw arcs from each end of the base to locate the vertex, ensuring symmetry.
- Join the ends of the base to the vertex point to form the isosceles triangle.
📐 Note: Understanding how to construct isosceles triangles manually can enhance your spatial visualization skills, which are crucial for advanced geometry.
Tip 4: Solve for Unknowns Using Given Information

Worksheet questions often require you to find missing angles, sides, or height:
- If you know the base, one side, and one angle, you can apply trigonometric functions or the Pythagorean Theorem to find other measures.
- For height, use the formula derived from the area or the properties of the median.
Example: Given base AB = 8 cm, side AC = 5 cm, and angle A = 40°, find the height:
- The perpendicular bisector from vertex A to the midpoint of AB will split the base in half (4 cm) and form a right triangle with the height.
- Using trigonometry, we find:
- Height = AC * sin(A) = 5 cm * sin(40°) ≈ 3.21 cm
Tip 5: Verify Your Work with Multiple Methods
Ensuring accuracy is key when working through geometric problems. Here are methods to cross-check your solutions:
- Use trigonometric identities to verify angles and sides.
- Calculate the area of the triangle using different formulas.
- Sum up the angles to confirm they total 180°.
- Check if your measures fit the isosceles triangle’s inherent symmetry.
🔎 Note: Always take the time to verify your results using at least two different methods or approaches to ensure your calculations are correct.
By following these tips, you'll be well-prepared to tackle isosceles triangle worksheet problems with confidence. Understanding the underlying principles and properties of isosceles triangles, utilizing theorems, and verifying your work will lead to mastery in this aspect of geometry. Remember, practice and patience are key to improvement, so keep working through exercises to sharpen your skills and deepen your understanding of geometric shapes.
What is the difference between an isosceles triangle and an equilateral triangle?

+
An isosceles triangle has at least two sides of equal length, while an equilateral triangle has all three sides of equal length. Consequently, all angles in an equilateral triangle are 60°, whereas in an isosceles triangle, only the base angles are equal.
How do I find the height of an isosceles triangle if I only know the base and one side?

+
You can use the Pythagorean Theorem in the right triangle formed by dropping a perpendicular bisector from the vertex to the midpoint of the base. The height, along with half the base and the known side, forms a right triangle where you can solve for the height using the theorem.
Can isosceles triangles have obtuse angles?

+
Yes, isosceles triangles can have obtuse angles, but only one angle can be obtuse because the sum of all three angles must equal 180°. If one angle is obtuse, the other two must be acute to maintain the sum.


