5 Proven Methods to Identify Function Intervals

The significance of function intervals in mathematics, particularly in calculus and algebra, cannot be overstated. They provide crucial insights into the behavior and characteristics of functions across different intervals. Identifying these intervals is not just an academic exercise but a practical skill beneficial in real-world applications such as engineering, finance, and statistics. Here are five proven methods to accurately determine function intervals:
1. Continuity Testing

Continuity is a fundamental property of functions in mathematics, which is often crucial when determining intervals:
- Check for continuity at specific points to ensure no gaps or jumps occur.
- Use the epsilon-delta definition of continuity if you are comfortable with the formalism.
- Graph the function and visually inspect for discontinuities:
Here, look for any points where the function is undefined, has vertical asymptotes, or exhibits jumps.

2. Derivative Analysis

Derivatives are key in understanding the rate of change and the local behavior of a function:
- Calculate the first derivative of the function to find critical points where the slope is zero or undefined.
- Determine whether the derivative is positive or negative over certain intervals to understand where the function is increasing or decreasing.
- Employ the second derivative to pinpoint inflection points and concavity changes:
The second derivative test provides insights into where the function is concave up or down, which is helpful for identifying intervals.

3. Sign Chart Method

Creating a sign chart can help visually organize the behavior of the function:
- List critical points (where the derivative is zero or undefined) on a number line.
- Test the sign of the derivative in intervals between these points.
- Use intervals where the sign is consistent to denote where the function behaves similarly.
This method is particularly useful when dealing with polynomial functions or rational functions.
| Interval | Sign of f’(x) | Function Behavior |
|---|---|---|
| (-∞, -2) | - | Decreasing |
| (-2, 1) | + | Increasing |
| (1, +∞) | - | Decreasing |

4. Concavity and Inflection Points

Analyzing concavity changes can identify where the function transitions from curving up to curving down:
- Compute the second derivative of the function.
- Find the points where the second derivative is zero or undefined (inflection points).
- Determine the concavity by testing the sign of the second derivative in intervals around inflection points.
This method helps in identifying intervals where the function has specific properties related to its curvature.
5. Asymptotic Behavior Analysis
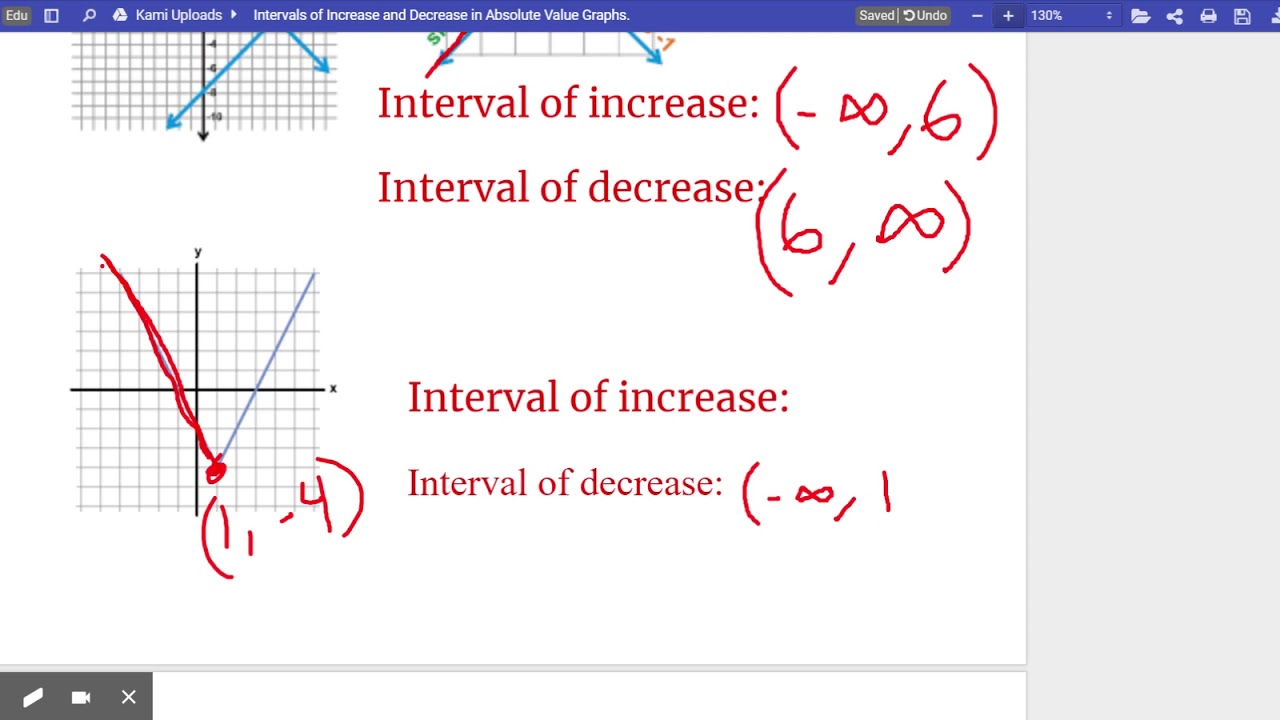
Asymptotes can dictate the behavior of functions at the extremes:
- Look for vertical asymptotes where the function approaches ±∞.
- Identify horizontal or oblique asymptotes to understand long-term behavior.
- Use the concept of limit at infinity to establish function intervals:
This method is crucial for functions that grow or decay without bound in certain directions.
💡 Note: The accuracy of your analysis largely depends on correctly identifying all relevant points and properly handling discontinuities.
By employing these methods, one can systematically and effectively analyze function intervals to provide a comprehensive understanding of a function’s behavior. Each approach complements the others, and often, using multiple methods will give a more complete picture. Understanding and applying these techniques are fundamental for solving various mathematical and real-world problems where functions play a pivotal role.
Remember, while these methods provide frameworks for analysis, the precise application can vary with each function's characteristics. Always verify your results by reviewing the function's graph, which can highlight overlooked behaviors or confirm your analytical findings.
Why is it important to identify function intervals?

+
Identifying function intervals allows for understanding the behavior of a function, which is critical in optimization, curve sketching, and solving equations in real-world applications.
What does a sign chart show?

+
A sign chart illustrates where the function is increasing or decreasing by showing the sign of the first derivative across different intervals.
Can the concavity change at critical points?
+
While critical points often coincide with changes in concavity, they are not the only points where concavity changes. Inflection points where the second derivative is zero or undefined are the precise locations where concavity changes.


