5 Tips to Ace Free Particle Model Worksheet 1b

In the world of physics education, mastering the concepts associated with motion and forces can open up a whole new dimension of understanding the universe. One effective tool educators use is the Free Particle Model Worksheet 1b, which focuses on kinematic motion and the basic principles of particle dynamics. Here are five essential tips to help students excel in completing this worksheet and enhancing their grasp of physics concepts.
Tip 1: Understand the Basics of Motion

Before delving into the worksheet, ensure you have a firm grasp on fundamental motion concepts:
- Speed and Velocity: Remember, velocity is a vector quantity; it has magnitude and direction. Speed is the scalar magnitude of velocity.
- Acceleration: Know how to calculate acceleration using the formula (a = \frac{\Delta v}{\Delta t}), where (\Delta v) is the change in velocity, and (\Delta t) is the change in time.

⚠️ Note: Pay attention to whether the problems on the worksheet ask for speed, velocity, or acceleration.
Tip 2: Master the Equations of Motion
Worksheet 1b will likely include problems that require you to use the kinematic equations:
- (v = u + at)
- [s = ut + \frac{1}{2}at^2]
- (v^2 = u^2 + 2as)
Knowing when to use which equation is critical:
| Equation | Use Case |
|---|---|
| (v = u + at) | When you know the initial velocity, acceleration, and time. |
| [s = ut + \frac{1}{2}at^2] | For problems involving displacement over a time period with uniform acceleration. |
| (v^2 = u^2 + 2as) | When acceleration, initial or final velocity, and displacement are known but time is unknown. |

💡 Note: Practice using these equations regularly to become familiar with their application.
Tip 3: Sketching Motion Diagrams
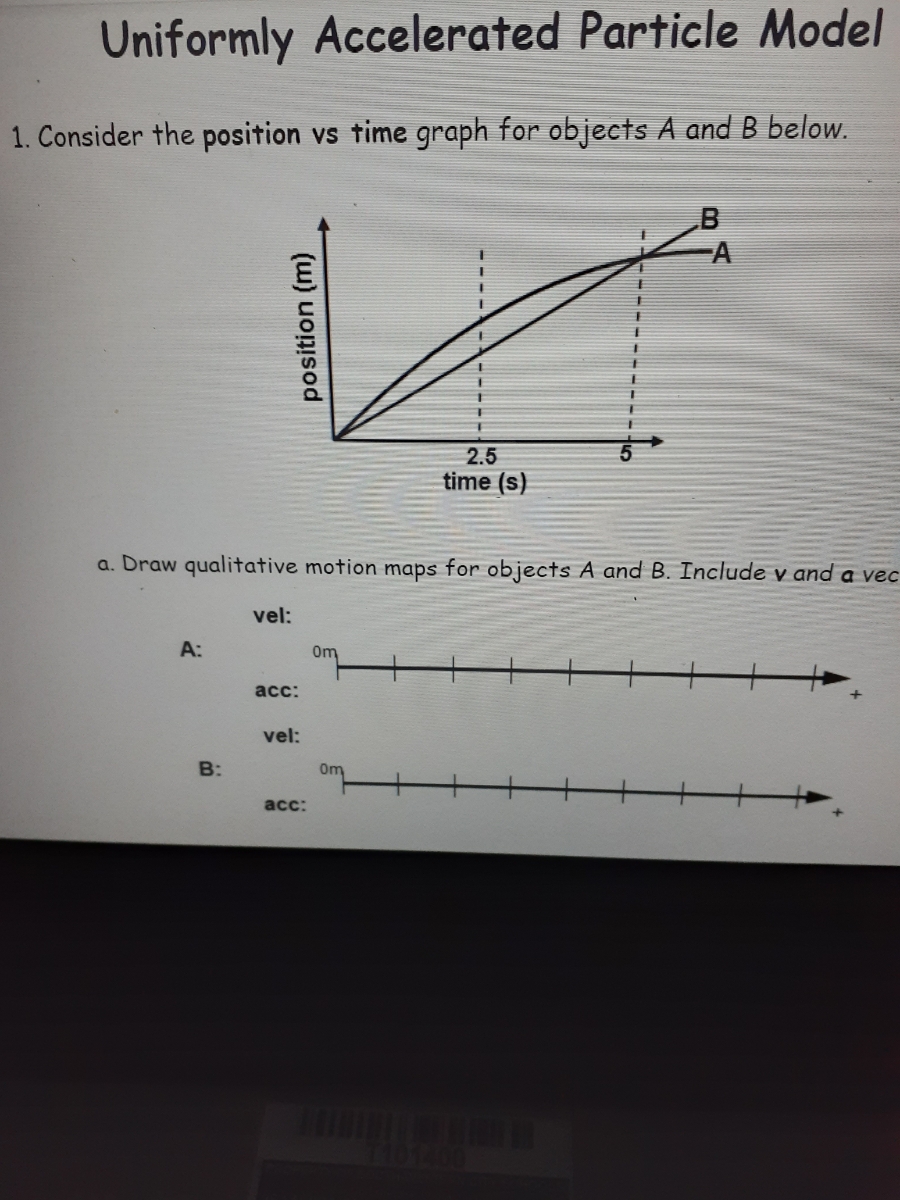
Often, visual representation can help in understanding complex motion problems:
- Draw a motion diagram for each object involved in the problem to visualize the movement over time.
- Mark the position, velocity vectors, and acceleration arrows if applicable.
- Check your drawn diagrams against your calculations to ensure consistency.

By creating these diagrams, you can better analyze and solve problems involving motion.
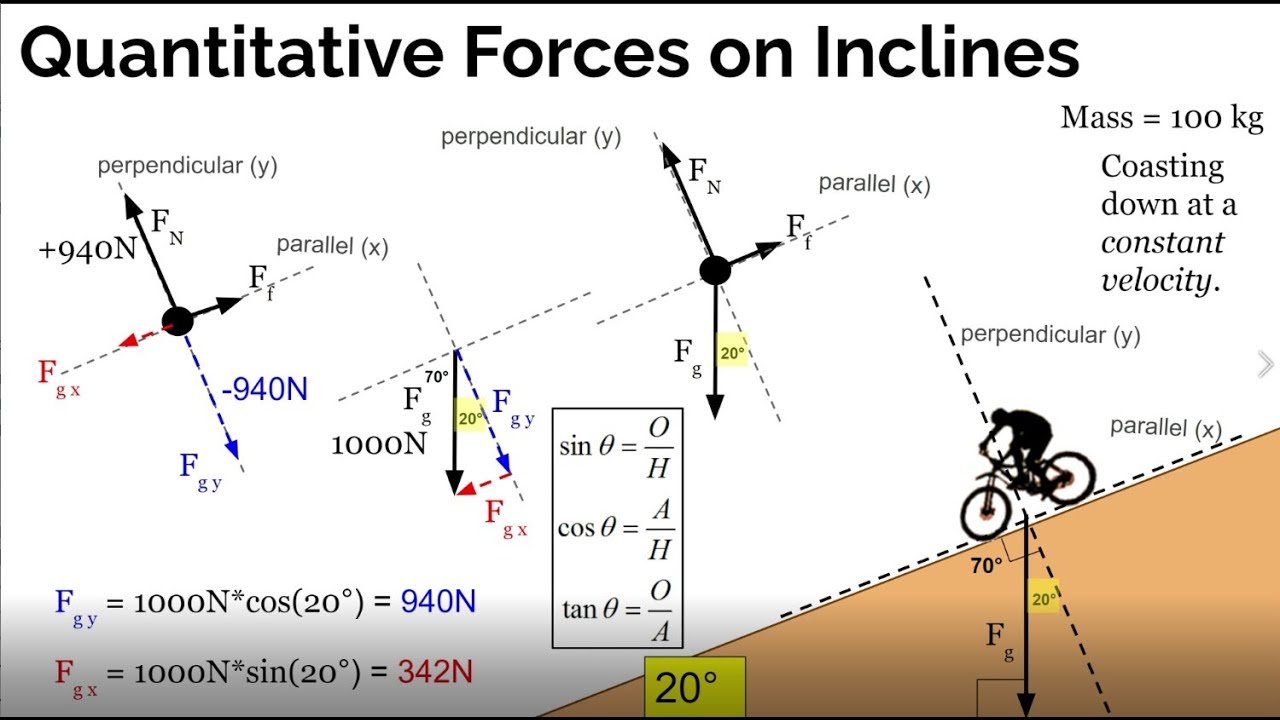
Tip 4: Use Free Body Diagrams

When forces are involved, sketching free body diagrams (FBD) can be very helpful:
- Identify all forces acting on the object of interest.
- Draw arrows representing the magnitude and direction of each force.
- Apply Newton’s Second Law ((F = ma)) using these diagrams to solve for unknowns.
These diagrams are particularly useful in problems where acceleration, net force, or individual forces need to be determined.

📍 Note: Practice drawing these diagrams until they become second nature.
Tip 5: Review and Learn from Mistakes

After completing the worksheet:
- Go through each problem and check your answers.
- Identify any mistakes in calculation, interpretation, or conceptual understanding.
- Make notes on where you went wrong, what the correct solution is, and how to avoid similar errors in the future.
This reflective practice is crucial for learning from errors and improving future performance.
Mastering the Free Particle Model Worksheet 1b involves not just solving equations but understanding the underlying principles of motion and force dynamics. By focusing on the fundamentals, practicing regularly, and learning from your errors, you'll develop a strong foundation in physics. This process will not only help you ace the worksheet but also build a deeper understanding that will serve you well in further studies or real-world applications. Remember, physics is not just about formulas; it's about visualizing the dance of forces and the elegance of motion in the universe.
What is the difference between speed and velocity?

+
Speed is a scalar quantity representing the rate of distance traveled per unit of time, whereas velocity is a vector quantity that includes both speed and direction.
How do I know which kinematic equation to use?

+
The choice of kinematic equation depends on the known quantities in the problem. For example, if you know the initial velocity, acceleration, and the time, you’d use (v = u + at).
Why are motion diagrams important?

+
Motion diagrams help visualize the motion over time, making it easier to understand and analyze complex problems by representing positions, velocities, and accelerations.