Mastering Inequalities on a Number Line Made Easy
Understanding Inequalities on a Number Line

Inequalities are a fundamental concept in mathematics, and visualizing them on a number line can make them easier to understand. A number line is a graphical representation of numbers on a line, with each point corresponding to a specific value. In this article, we will explore how to master inequalities on a number line, making it easier to solve problems and understand mathematical concepts.
What are Inequalities?

Inequalities are statements that compare two values, indicating that one value is greater than, less than, or equal to another value. The most common inequality symbols are:
- Greater than (>)
- Less than (<)
- Greater than or equal to (≥)
- Less than or equal to (≤)
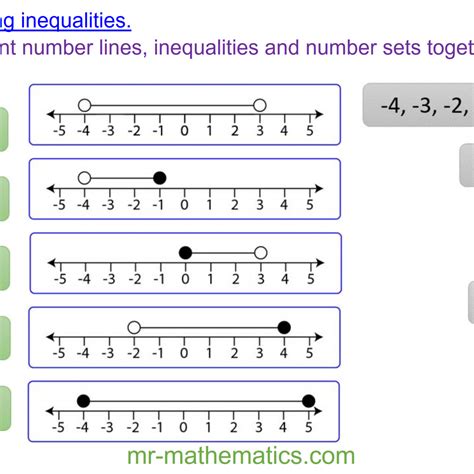
Visualizing Inequalities on a Number Line

To visualize inequalities on a number line, we can use the following steps:
- Draw a number line: Start by drawing a number line with equally spaced tick marks, each representing a specific value.
- Plot the values: Plot the values being compared on the number line.
- Determine the direction: Determine the direction of the inequality symbol. If the inequality symbol points to the right, the solution set will be to the right of the plotted value. If it points to the left, the solution set will be to the left.
- Shade the solution set: Shade the solution set on the number line, indicating the values that satisfy the inequality.
Examples of Inequalities on a Number Line

Let’s consider some examples of inequalities on a number line:
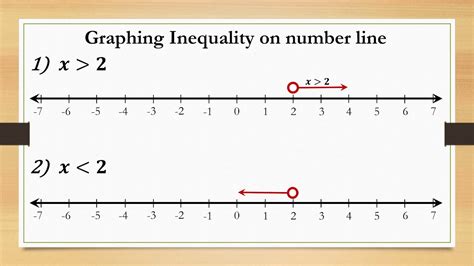
- Example 1: x > 3
To visualize this inequality, we plot the value 3 on the number line and shade the area to the right, indicating that x can be any value greater than 3.
- Example 2: x ≤ 5
To visualize this inequality, we plot the value 5 on the number line and shade the area to the left, including the value 5, indicating that x can be any value less than or equal to 5.
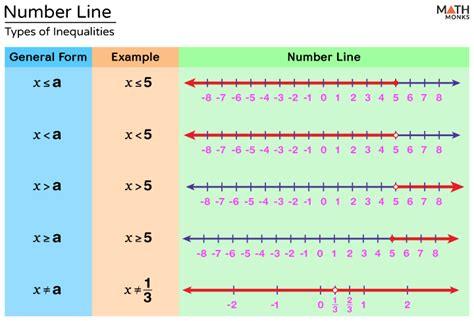
Types of Inequalities

There are two main types of inequalities:
- Linear inequalities: These involve a linear expression on one side of the inequality symbol and a constant value on the other side. For example: 2x + 3 > 5.
- Nonlinear inequalities: These involve a nonlinear expression on one side of the inequality symbol and a constant value on the other side. For example: x^2 + 3x > 5.
Solving Inequalities on a Number Line

To solve inequalities on a number line, we can follow these steps:
- Simplify the inequality: Simplify the inequality by combining like terms and isolating the variable.
- Plot the values: Plot the values being compared on the number line.
- Determine the direction: Determine the direction of the inequality symbol.
- Shade the solution set: Shade the solution set on the number line, indicating the values that satisfy the inequality.
Common Mistakes to Avoid
When working with inequalities on a number line, it’s essential to avoid common mistakes, such as:
- Reversing the inequality symbol: Make sure to maintain the correct direction of the inequality symbol.
- Not including the endpoint: When shading the solution set, make sure to include the endpoint if the inequality symbol includes an equal sign.
📝 Note: When solving inequalities, it's essential to check your solution by plugging in test values to ensure the solution set is correct.
Conclusion
Mastering inequalities on a number line requires practice and patience. By following the steps outlined in this article and avoiding common mistakes, you can become proficient in solving inequalities and visualizing them on a number line. Remember to always check your solution by plugging in test values to ensure accuracy.
What is the difference between an equal sign and an inequality symbol?

+
An equal sign (=) indicates that two values are equal, while an inequality symbol (>, <, ≥, ≤) indicates that one value is greater than, less than, or equal to another value.
How do I determine the direction of an inequality symbol?

+
To determine the direction of an inequality symbol, look at the symbol itself. If the symbol points to the right, the solution set will be to the right of the plotted value. If it points to the left, the solution set will be to the left.
What is the purpose of shading the solution set on a number line?

+
Shading the solution set on a number line helps to visualize the values that satisfy the inequality, making it easier to understand and work with the solution.
Related Terms:
- Inequalities Worksheet PDF with answers
- inequalities worksheets with answer key
- inequalities exercises with answers
- free work sheets on inequalities
- show inequality on number line
- solving inequalities worksheet with answers



