5 Tips for Mastering Graphing Standard Form

When you encounter problems with graphing standard form equations of lines in algebra or geometry, it might seem overwhelming. However, with the right approach and understanding, you can master the art of graphing standard form. Here are five comprehensive tips to guide you:
1. Understanding Standard Form


Before you dive into graphing, it’s vital to know what the standard form of a linear equation looks like. The standard form is typically written as:
Ax + By = C
- A, B, C - Constants where A and B are not both zero.
- x - x-coordinate on the plane
- y - y-coordinate on the plane
🔑 Note: Ensure that A is positive and both A and B are integers to keep the equation in standard form.
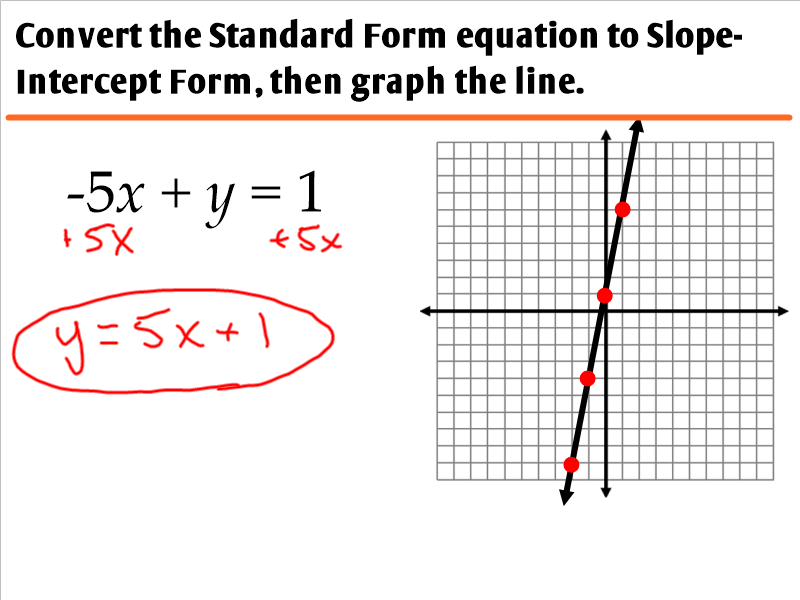
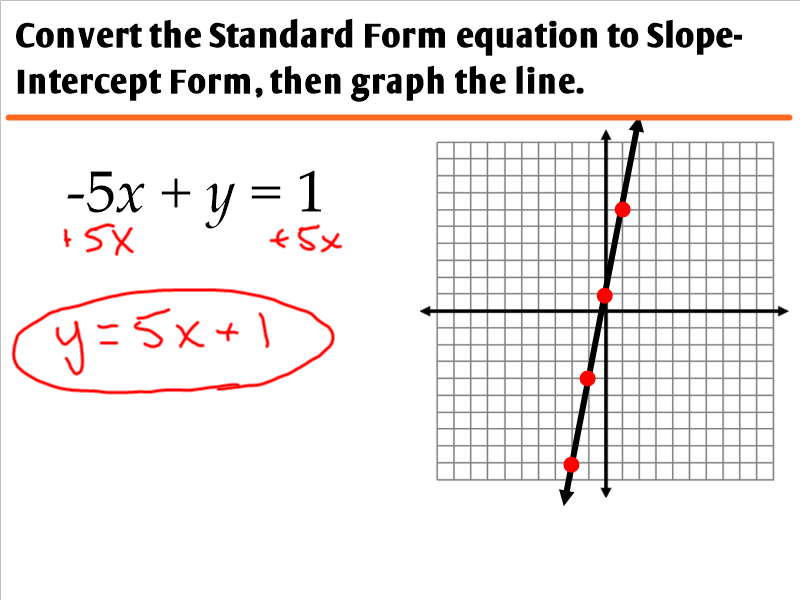
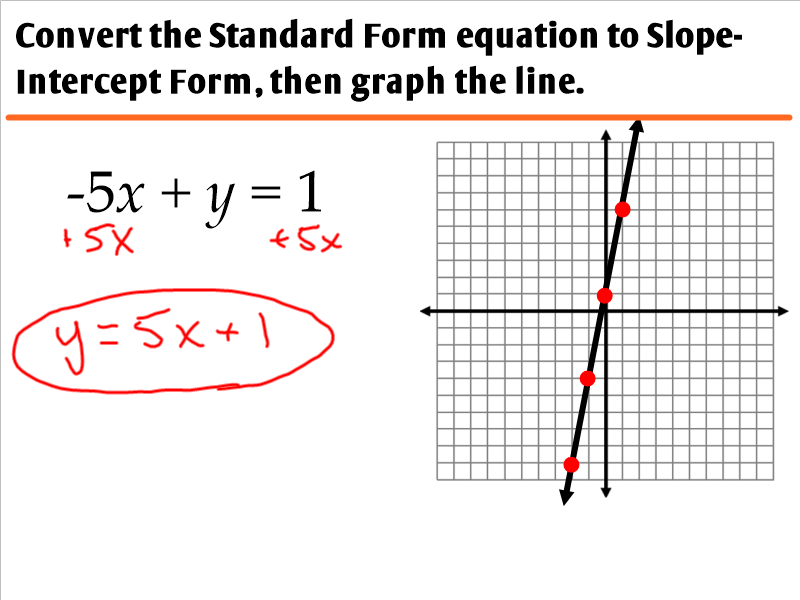
2. Converting Standard Form to Slope-Intercept Form

To make graphing easier, one of the most effective strategies is converting standard form to slope-intercept form:
- Start with the equation in standard form: Ax + By = C
- Isolate y:
- Subtract Ax from both sides: By = -Ax + C
- Divide everything by B to solve for y:
- Now you have the equation in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept.
y = -(A/B)x + (C/B)
🔑 Note: The fraction m = -(A/B) might not always be in its simplest form; simplify if possible to make graphing easier.
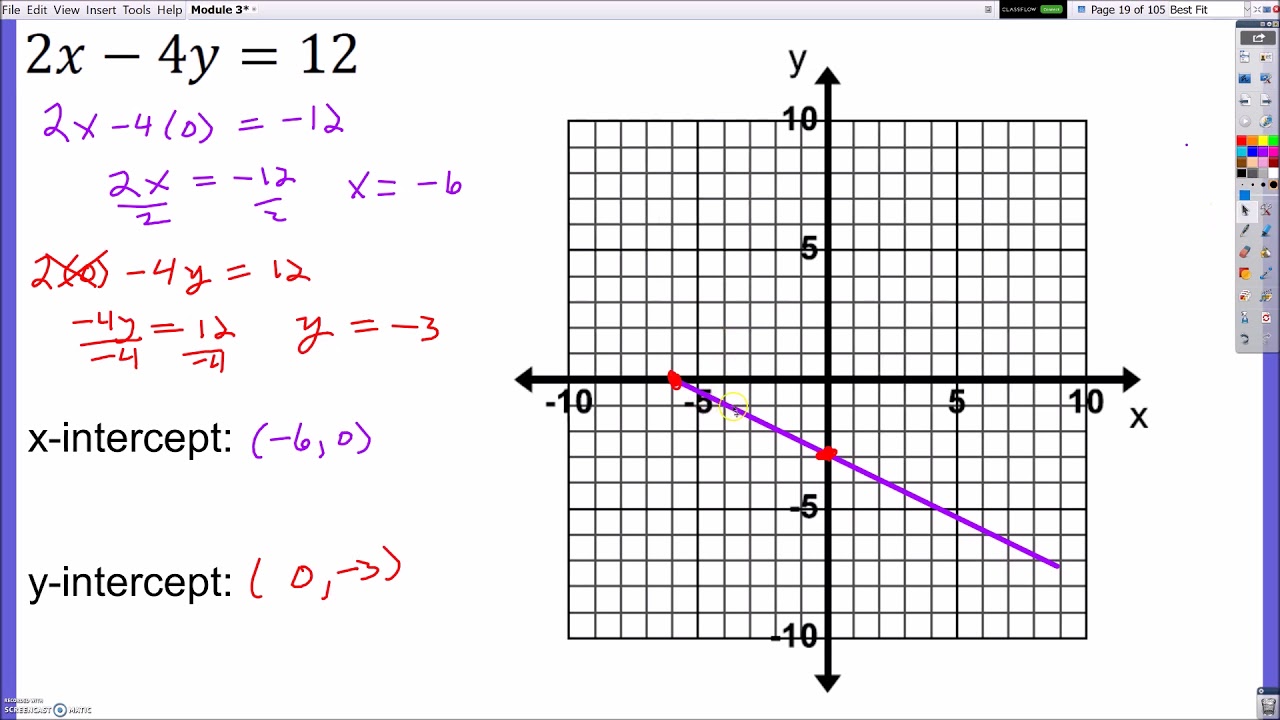
3. Using Intercepts for Quick Plotting
| Intercept | How to Find |
|---|---|
| x-intercept | Set y = 0 and solve for x |
| y-intercept | Set x = 0 and solve for y |
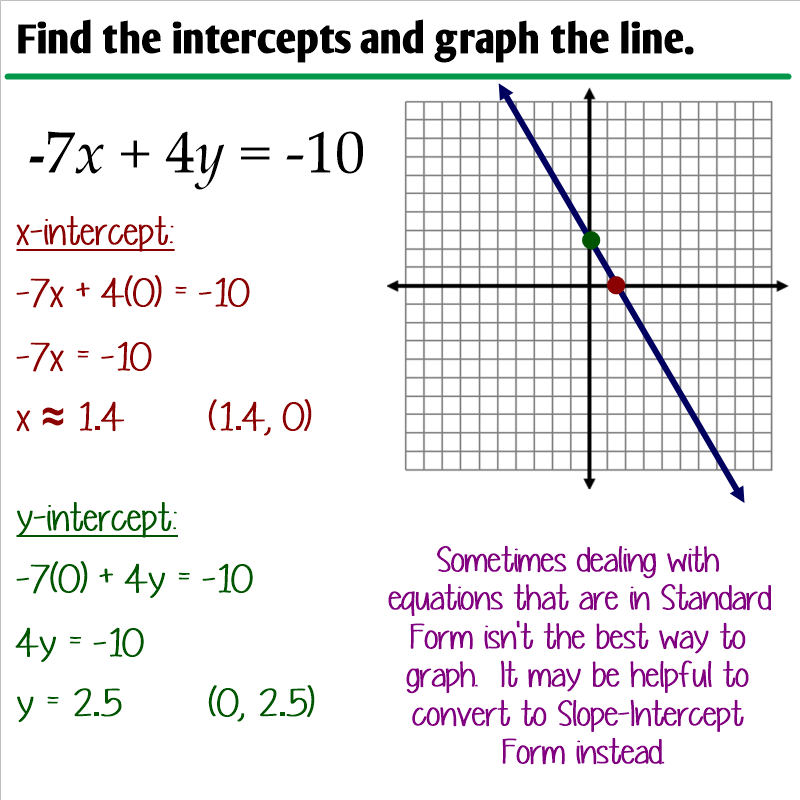
You can plot the intercepts directly:
- x-intercept: Substitute y = 0 in Ax + By = C and solve for x.
- y-intercept: Substitute x = 0 in Ax + By = C and solve for y.
- After finding the intercepts, draw a straight line passing through both points on the graph.
4. Employing Technology for Verification
Graphing calculators or software can be invaluable tools:
- Enter the standard form equation into the graphing calculator or software.
- Check if the graph matches what you’ve plotted manually.
- This can help you spot mistakes or understand where you might have misinterpreted the equation.
🔑 Note: While technology is helpful, it should not replace understanding the mathematical process; use it as a check, not a substitute for learning.
5. Practice with a Variety of Examples

To truly master graphing, practice is key:
- Start with simple equations like 2x + y = 4.
- Move on to more complex equations that involve larger numbers or coefficients.
- Include negative coefficients to understand how they affect the graph.
🔑 Note: Regular practice will make you quicker at recognizing patterns and solving for intercepts.
In closing, mastering graphing standard form involves a deep understanding of how to manipulate equations, find intercepts, use technology, and practice extensively. By internalizing these tips, you’ll find yourself effortlessly navigating through graphing challenges, making algebra and geometry more approachable and less daunting. Each tip provides a building block towards fluency in graphing, so integrate them into your study routine, and watch your confidence in this area grow.
Why is the standard form important?
+
Standard form is often used in applications like linear programming or when dealing with systems of equations. It provides a consistent way to compare and manipulate equations.
Can I graph standard form without converting?

+
Yes, you can find the intercepts directly from standard form, making it possible to graph without converting to slope-intercept form, although it might be less intuitive for beginners.
What if the equation isn’t linear?
+
If the equation involves powers higher than one (like x^2 or y^2), you’re dealing with a nonlinear equation, which requires different graphing methods like factoring or using conic sections.
How can technology help in graphing?

+
Graphing tools can plot lines, find intercepts, and check your work, providing a visual representation that can be compared with manual plotting to ensure accuracy.



