5 Essential Tips for Graphing Linear Inequalities Worksheet Answers

5 Essential Tips for Graphing Linear Inequalities Worksheet Answers
Understanding how to graph linear inequalities is a fundamental skill in algebra and beyond. Whether you're a student looking to improve your grades or a teacher seeking ways to explain this concept effectively, mastering the art of graphing inequalities can open doors to solving complex real-world problems. In this detailed guide, we'll delve into five essential tips to make graphing linear inequalities worksheets answers easier, more intuitive, and accessible.
The Concept Behind Linear Inequalities


Linear inequalities are statements comparing an expression using symbols like <, >, <=, >=. Unlike linear equations, inequalities express a range of solutions that can be represented on a graph. Here’s how to understand and graph them:
- Understand the inequality symbols: Each symbol determines how the solutions are shaded on the graph.
- Convert to slope-intercept form: Transform inequalities into the form y = mx + b or y < mx + b to simplify graphing.
- Graph the line: Determine if the line should be dashed (for < or >) or solid (for <= or >=).
- Shade the appropriate region: Above or below the line, depending on the inequality sign.
- Check a test point: To confirm the correct region has been shaded.
Tip 1: Identify the Inequality Type

The first step in solving and graphing linear inequalities is recognizing the type of inequality you are dealing with:
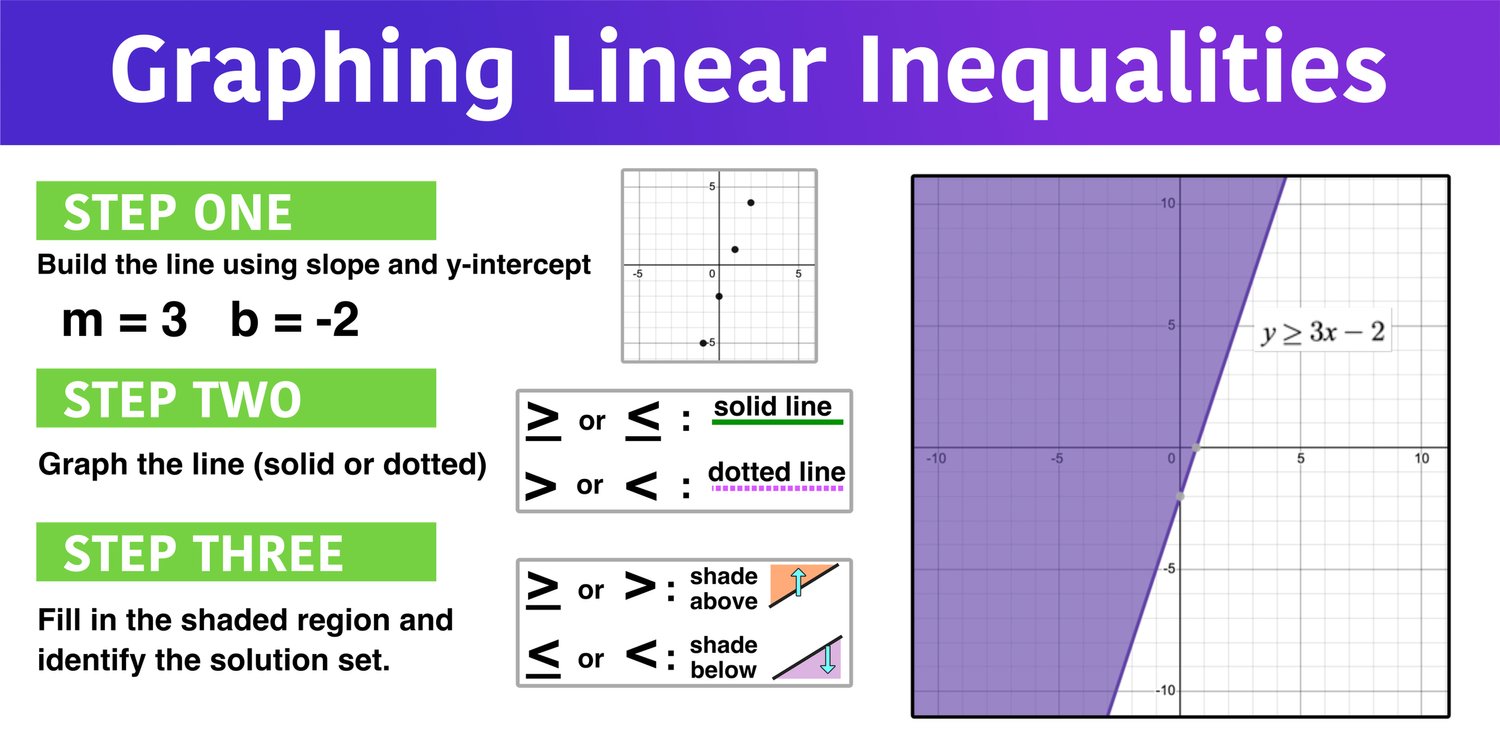
- Strict inequalities ( <, >) indicate that the boundary line is not included in the solution set. This means the graph should use a dashed line.
- Inclusive inequalities ( <=, >=) show that the boundary line is part of the solution set, requiring a solid line on the graph.
| Inequality Type | Graph Style | Example |
|---|---|---|
| Strict (< or >) | Dashed Line | y < 2x + 3 |
| Inclusive (<= or >=) | Solid Line | y >= 2x + 3 |

💡 Note: Recognizing the inequality type is crucial for accurately interpreting and graphing the solution set.
Tip 2: Understand the Slope-Intercept Form

Graphing becomes significantly easier when you convert the inequality into slope-intercept form. Here’s how to do it:
- Isolate y on one side of the inequality.
- Divide or multiply by the same factor on both sides if needed.
- Identify m (slope) and b (y-intercept).
Once in this form, you can graph the line with m dictating the line’s rise and run, and b showing where the line crosses the y-axis.
Tip 3: Graph the Line Correctly

After converting to slope-intercept form:
- Plot the y-intercept: Use the b value to plot where the line touches the y-axis.
- Use the slope: Count the rise and run from the y-intercept to draw the line.
- Dashed or Solid: Use a dashed line for strict inequalities or a solid line for inclusive inequalities.
🔔 Note: When the inequality involves more than one line, ensure to plot and shade each inequality correctly to find the intersection area.
Tip 4: Shade the Appropriate Region

Shading correctly determines where the solutions to the inequality lie:
- For inequalities like y < mx + b, shade below the line.
- For inequalities like y > mx + b, shade above the line.
A handy trick is to use a test point. Select any point (like (0,0) if it’s not on the line) and plug it into the inequality. If the inequality is satisfied, shade the region containing this test point.
Tip 5: Double-Check Your Work

After graphing:
- Check your shading: Ensure you’ve shaded the correct region.
- Examine the boundary lines: Make sure you’ve drawn dashed lines for strict inequalities and solid for inclusive ones.
- Verify the solution set: Using a different test point or solving the inequality for a few values to confirm the graph.
👓 Note: Precision in graphing is key to solving inequalities correctly. Take your time to ensure accuracy.
In summary, graphing linear inequalities involves understanding the inequality type, converting to slope-intercept form, drawing the line with the correct style, shading the appropriate region, and double-checking your work. With these five tips, you'll be well-equipped to handle any graphing linear inequalities worksheet answers effectively. The journey of graphing linear inequalities isn't just about mastering algebraic concepts; it's about developing a visual understanding of how numbers and variables interact in the realm of algebra, laying a foundation for more advanced mathematical exploration.
What is the difference between strict and inclusive inequalities in graphing?
+
Strict inequalities (< or >) indicate that the boundary line is not part of the solution set and should be represented by a dashed line. Inclusive inequalities (=< or =>) show that the boundary line is included, and thus, they require a solid line in the graph.
Why is converting to slope-intercept form helpful?

+
Converting an inequality to slope-intercept form makes it easier to identify the line’s slope (m) and y-intercept (b), simplifying the process of graphing the line. It’s a standard form that provides clear insights into the line’s behavior.
How do you shade regions for inequalities?
+
The direction of shading depends on the inequality symbol. For inequalities like y < mx + b, you shade below the line; for y > mx + b, you shade above the line. Using a test point can confirm you’ve shaded the right region.



