5 Tips to Graph Parabolas Easily from Vertex Form

Understanding how to graph parabolas is crucial for anyone studying algebra or higher mathematics. While there are various forms of quadratic equations, the vertex form, y = a(x - h)² + k, provides a straightforward way to locate the vertex and sketch the parabola with precision. Here are five tips to master graphing parabolas from their vertex form.
1. Identify the Vertex

The first step in graphing a parabola in vertex form is to identify its vertex. The vertex form directly tells you the coordinates of the vertex. For an equation like:
y = a(x - h)² + k
the vertex is at (h, k). Here, h indicates the horizontal shift, and k indicates the vertical shift from the origin. For example, in y = 2(x - 3)² + 5, the vertex is at (3, 5).
🔍 Note: Remember, h is the negative of what it appears in the equation due to the form.
2. Determine the Direction of the Parabola

The coefficient a in the vertex form equation determines whether the parabola opens upwards or downwards:
- If a > 0, the parabola opens upwards.
- If a < 0, the parabola opens downwards.
This information, combined with the vertex, helps you plot the basic shape of the parabola.
3. Use Symmetry

Parabolas are symmetrical about their axis of symmetry, which passes through the vertex. The equation for the axis of symmetry in vertex form is x = h. Use this line as a guide to plot points on either side of the vertex for a balanced graph. For example, if h=3, plot points at x=2 and x=4, then find the corresponding y-values.
4. Choose Additional Points

After establishing the vertex and the direction, select two or three more points to get a more accurate representation of the parabola’s shape:
- Find the y-intercept by setting x to 0.
- Choose symmetric x-values around the vertex to calculate corresponding y-values. For instance, if your vertex is at (3,5), you could choose x = 2, x = 4 for symmetry.
💡 Note: Choosing points near the vertex helps to see the shape close to the vertex accurately.
5. Adjust for Scaling

The value of a affects how wide or narrow the parabola is:
- If |a| > 1, the parabola will be narrower.
- If |a| < 1, the parabola will be wider.
Adjust the scale of your graph accordingly to depict this stretch or compression accurately.
To wrap up, mastering the vertex form of parabolas not only makes graphing simpler but also helps in understanding the underlying properties of quadratic functions. It's a fundamental skill in algebra that opens the door to deeper insights into mathematical analysis.
Having a grasp on these tips not only simplifies your graphing but enhances your understanding of how parabolas behave in different scenarios. Whether you're tackling complex problems or just curious about the behavior of these curves, these techniques will serve as a reliable guide.
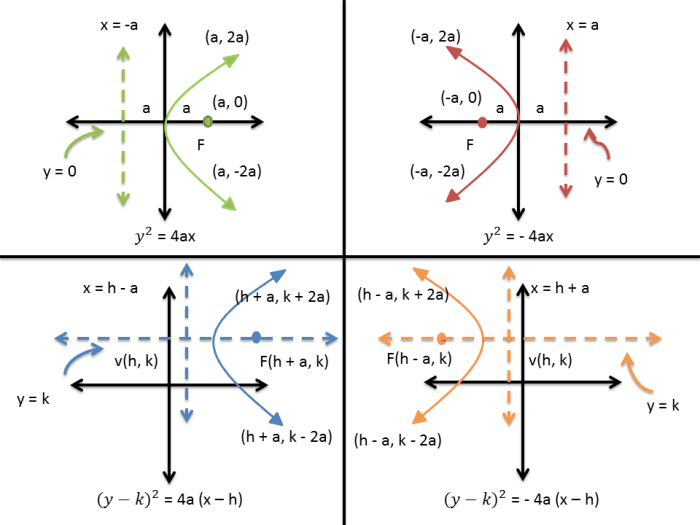
Why is the vertex form advantageous for graphing parabolas?
+
The vertex form directly gives you the vertex of the parabola, which is a critical point for graphing. It simplifies the process by immediately providing the vertex coordinates and the direction in which the parabola opens.
Can parabolas open horizontally in vertex form?
+
No, parabolas in vertex form only open vertically. To graph parabolas that open horizontally, you would need to use the standard or intercept form of the quadratic equation.
What if the vertex form includes fractions for h and k?

+
If h and k are fractions, they still indicate the coordinates of the vertex. You would simply plot these fractional values on your graph, keeping in mind that they will shift the vertex accordingly.
How does changing the value of a affect the parabola?
+
The coefficient a affects both the direction and the width of the parabola. A positive a makes the parabola open upward, and a negative a downward. The larger the absolute value of a, the narrower the parabola; the smaller, the wider.



