Integer Review Worksheet: Master Your Number Skills Now

Welcome to our comprehensive guide on mastering your integer skills. Integers are the foundation of mathematical operations, and a strong grasp of them is crucial for both everyday tasks and complex mathematical problems. In this article, we'll delve into a thorough review of integer operations, ensuring you leave with an unwavering confidence in handling these fundamental numbers.
Understanding Integers

Integers are the set of whole numbers, which includes positive numbers, negative numbers, and zero. They do not include fractions or decimals. Here’s a quick refresher on integers:
- Positive Integers: 1, 2, 3, … (They go on infinitely.)
- Negative Integers: -1, -2, -3, … (They also extend infinitely in the opposite direction.)
- Zero: Often considered a placeholder or null in many contexts.

📝 Note: Zero is considered an integer but is neither positive nor negative.
Adding and Subtracting Integers

The rules for adding and subtracting integers are straightforward once you understand the concept of opposites:
- Positive + Positive: Add the numbers normally. E.g., 4 + 5 = 9
- Negative + Negative: Add the absolute values and make the result negative. E.g., (-4) + (-5) = -9
- Positive + Negative: Subtract the smaller number from the larger, then take the sign of the number with the greater absolute value. E.g., 4 + (-7) = -3
- Subtracting a Negative: Essentially adds a positive number. E.g., 5 - (-3) = 5 + 3 = 8
| Operation | Example | Result |
|---|---|---|
| Positive + Positive | 4 + 5 | 9 |
| Negative + Negative | (-4) + (-5) | -9 |
| Positive + Negative | 4 + (-7) | -3 |
| Subtracting a Negative | 5 - (-3) | 8 |

Multiplying and Dividing Integers

The signs of the results in multiplication and division are determined by the signs of the operands:
- Positive * Positive or Negative * Negative: The result is Positive. E.g., 4 * 5 = 20, (-4) * (-5) = 20
- Positive * Negative or Negative * Positive: The result is Negative. E.g., 4 * (-5) = -20, (-4) * 5 = -20
- Dividing: Follows the same rules. E.g., 10 ÷ 5 = 2, 10 ÷ (-5) = -2
💡 Note: The multiplication and division of integers always result in an integer, unless you're dealing with improper fractions or mixed numbers.
Order of Operations

When dealing with integers, the order of operations (PEMDAS/BODMAS) helps prioritize tasks:
- Parentheses / Brackets: Solve operations inside brackets first.
- Exponents / Orders: Deal with powers and square roots.
- Multiplication and Division: From left to right.
- Addition and Subtraction: Also from left to right.
Example: 3 + 4 * (2 - (-1)) = 3 + 4 * 3 = 3 + 12 = 15
Practice Exercises

To truly master integers, practice is key. Here are some exercises to reinforce what you’ve learned:
- Simplify the following: (a) 5 + (-9) + 10 (b) (-7) * (-3) + 6 © -20 ÷ (-4) - 5
- Create word problems involving integer operations and solve them.
🏋️ Note: Practice is essential. Start with simple exercises and gradually increase complexity.
Final Thoughts

Having walked through this extensive review, you’re now equipped with a deeper understanding and proficiency in integer operations. Whether for practical applications or academic pursuits, your newfound mastery will serve you well. Remember that consistent practice will solidify your skills, making integer calculations second nature. Always approach problems methodically, keeping in mind the rules and concepts outlined above, and you’ll find integer math not just manageable but enjoyable.
What is the difference between integers and whole numbers?

+
While all whole numbers are integers, not all integers are whole numbers. Integers include all whole numbers (0, 1, 2, …) and their negative counterparts (-1, -2, …), whereas whole numbers only include positive numbers and zero.
How do I know when to add or subtract integers?

+
Adding integers involves the following rules: positive + positive or negative + negative equals a result of the same sign, while adding a positive and a negative involves subtraction. Subtracting a negative number from a positive or vice versa essentially adds a positive number.
Why does multiplying two negatives give a positive result?

+
The convention that negative times negative equals positive has a foundation in the concept of opposites. If you multiply a negative number (representing a loss) by another negative number (another loss), you’re essentially recovering the initial loss, which means a gain or positive result.
What are some real-life applications of integers?
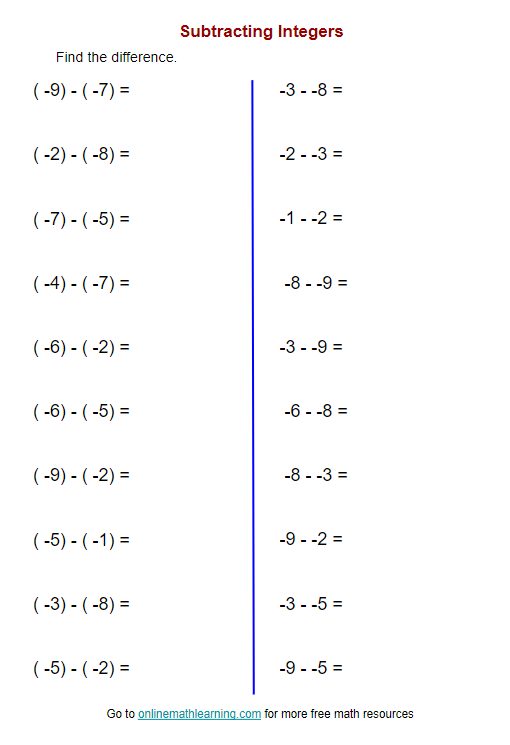
+
Integers are used in finance (bank balances), temperatures (above or below zero), elevation measurements (above sea level or below), game scores, and more.