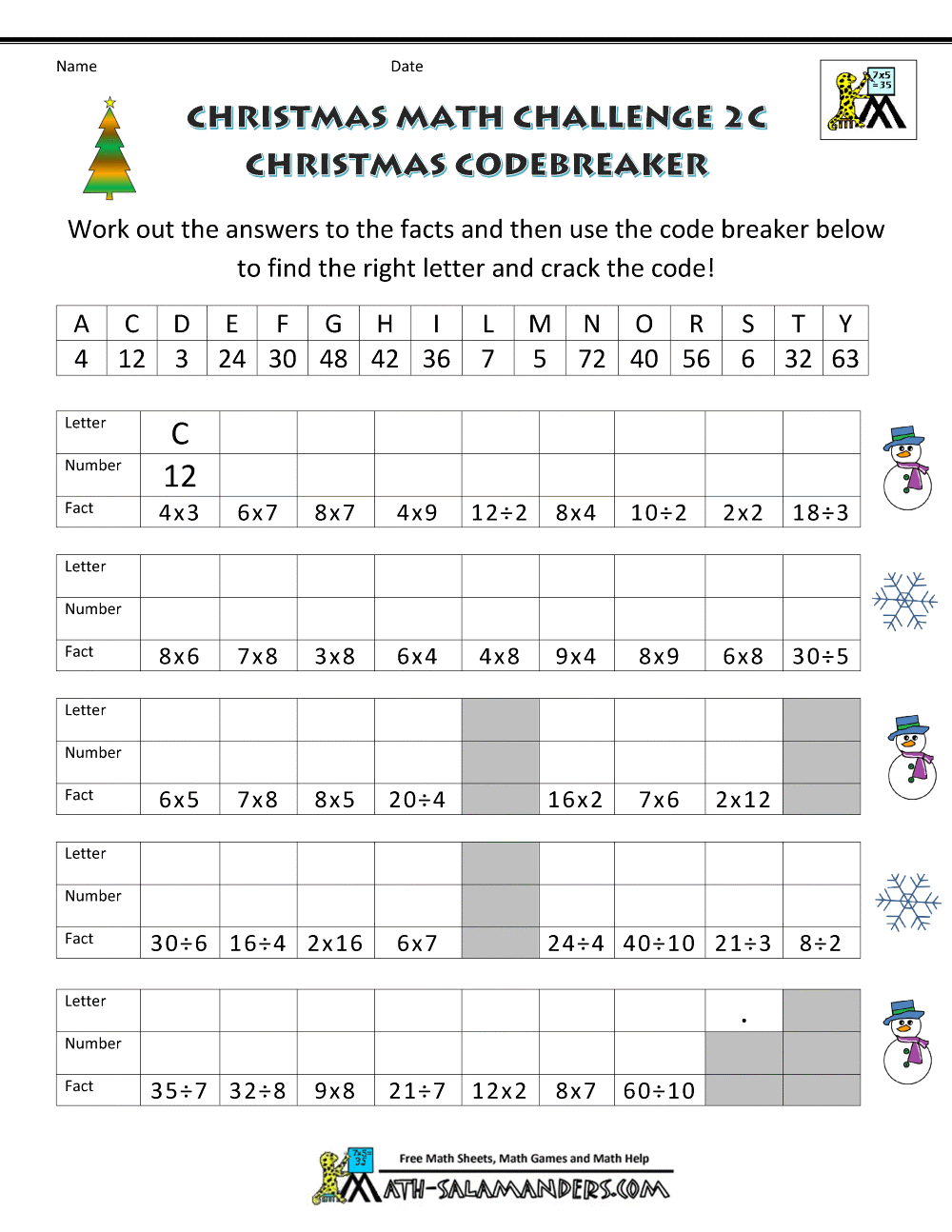
5 Simple Ways to Graph Lines with Slope and Point

The art of graphing lines in the coordinate plane is a foundational skill in mathematics, essential for understanding various algebraic concepts. If you're exploring how to graph lines using the slope-intercept form, two-point method, or other strategies, this comprehensive guide will elucidate five simple yet effective ways to graph lines with given slopes and points, ensuring clarity in your mathematical endeavors.
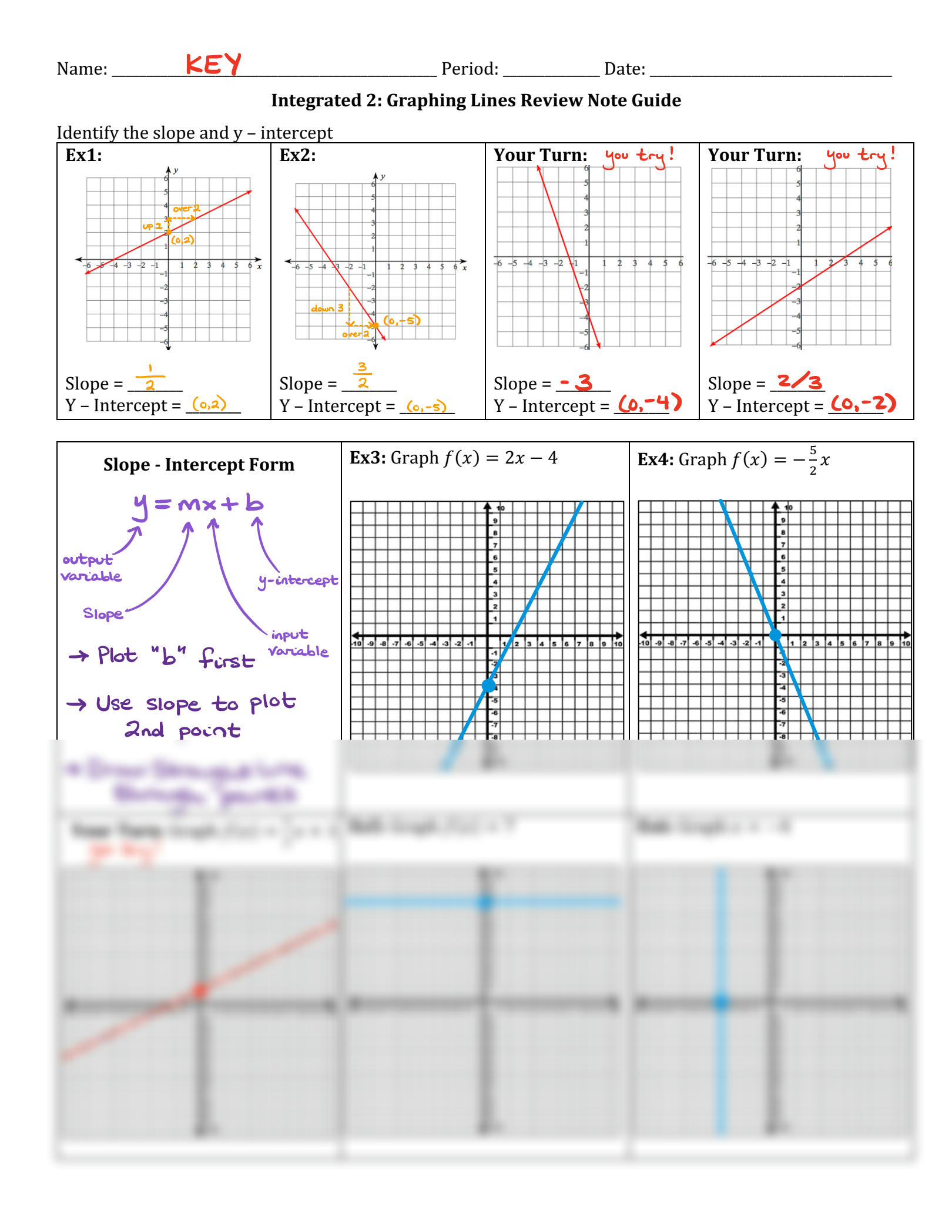
1. Using the Slope-Intercept Form

Perhaps the most commonly recognized method involves using the equation y = mx + b where m represents the slope and b the y-intercept.
- Identify the Slope (m): Determine the rise and run from the slope given.
- Locate the y-Intercept (b): Plot this point on the y-axis.
- Plot a Second Point: Using the slope, move from the y-intercept to another point.
- Connect the Points: Draw a line through these points.
🚦 Note: This method is particularly useful when the y-intercept and slope are directly given.
2. Two-Point Method

When you have two distinct points on a line, here’s how to graph it:
- Plot Points: Mark the given points on the coordinate plane.
- Calculate Slope: Use the slope formula (m = (y2 - y1) / (x2 - x1)).
- Connect with a Line: Draw a straight line through these points.
| Point 1 | Point 2 | Slope (m) |
|---|---|---|
| (1, 2) | (5, 6) | (6 - 2) / (5 - 1) = 1 |

📝 Note: The two-point method allows you to find the line's direction without needing the equation in slope-intercept form.
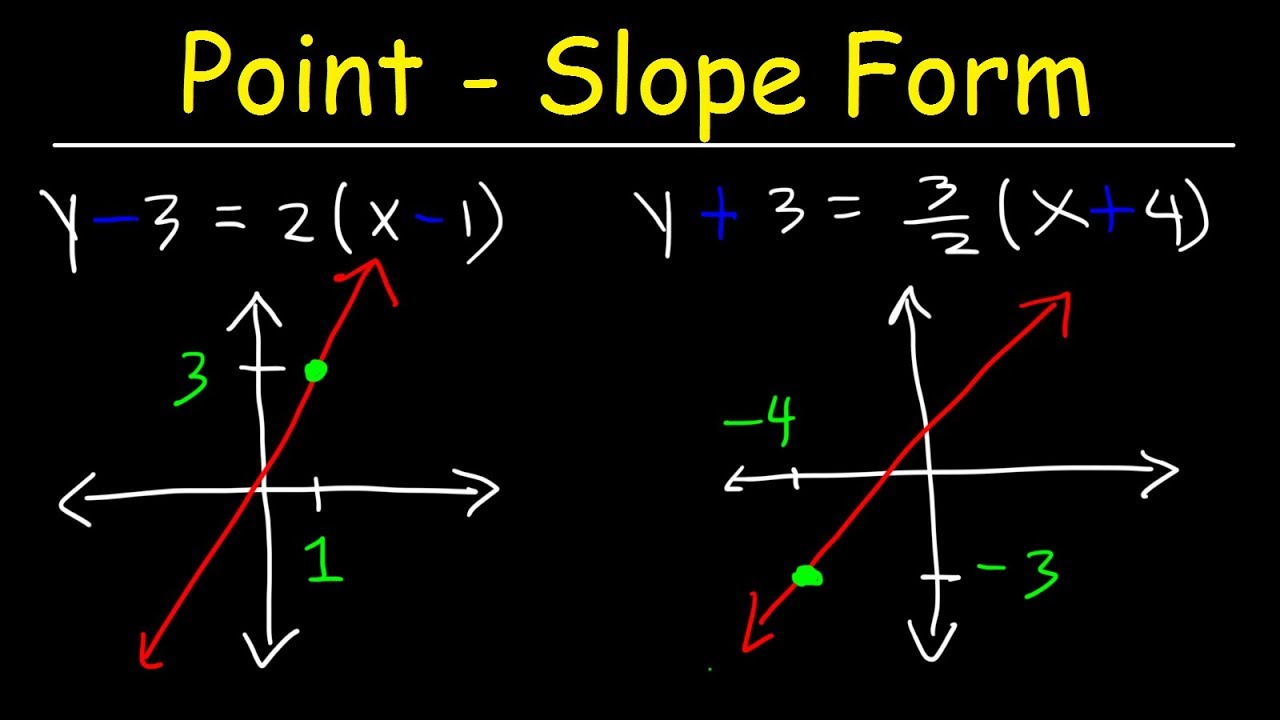
3. Point-Slope Form

If you have a single point (x1, y1) and the slope m, use the point-slope form of the line equation, y - y1 = m(x - x1):
- Identify Slope and Point: You're given or can calculate these values.
- Substitute into the Equation: Use these values to write the equation.
- Plot Points and Graph: From the given point, use the slope to plot another point, then draw the line.
4. Using a Table of Values

Generating a table of values can be especially helpful when dealing with non-linear functions or when exact forms are cumbersome:
- Choose x Values: Pick convenient x values to start with.
- Calculate Corresponding y Values: Use the given equation or slope-point relationship to find y.
- Plot Points: Mark these points on the coordinate plane.
- Draw the Line: Connect the plotted points to graph the line.
| x | y = 2x + 3 |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
5. Utilizing Technology

In today’s digital age, you can leverage technology for graphing:
- Graphing Calculators: Input the equation, and let the calculator do the work.
- Online Graphing Tools: Websites like Desmos offer interactive graphing capabilities.
- Software like GeoGebra: Create and manipulate dynamic math models.
💡 Note: While technology is helpful, understanding the basic principles ensures you can graph manually when needed.
In summary, we've explored five straightforward methods for graphing lines with given slopes and points. Each approach provides unique advantages, from immediate plotting using slope-intercept form to leveraging technology for precise calculations. Whether you're tackling homework, preparing for an exam, or engaging in real-world applications, these techniques will enhance your ability to visualize linear functions accurately. Remember, the more you practice, the more intuitive these processes will become, reinforcing your grasp of algebra and geometry concepts.
What if I only have one point and the slope?
+
Use the point-slope form to find another point and then graph the line as described in method 3.
How do I handle fractional slopes?

+
Convert the slope to a ratio and use that to plot additional points. For example, a slope of 1⁄2 means you go up 1 unit for every 2 units horizontally.
Can I use these methods for non-linear functions?
+
While the methods discussed here focus on linear functions, you can adapt the table of values method for non-linear functions by selecting different x values and calculating the corresponding y values.
What’s the best method for beginners?

+
Starting with the slope-intercept form or the two-point method can be the most intuitive for beginners due to their straightforward application.
Are there any advantages to using technology?
+
Yes, technology can quickly calculate points, provide an immediate visual representation, and facilitate exploring the effects of changing equations or parameters.