5 Ways to Master Complementary and Supplementary Angles

Mastering Complementary and Supplementary Angles: A Key to Unlocking Geometric Success
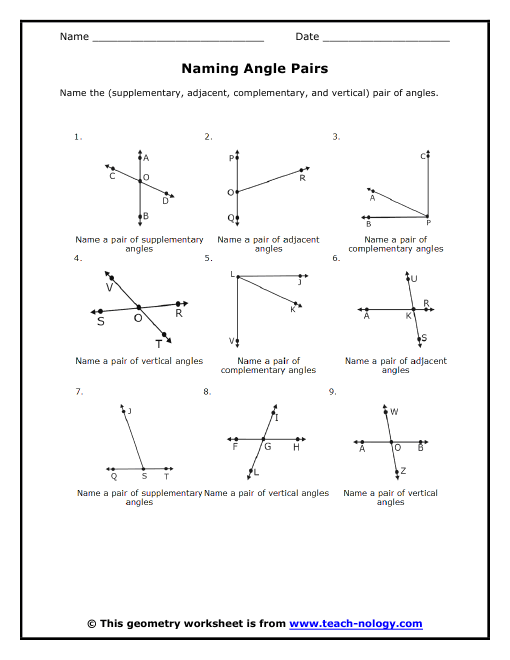
Geometry is a fundamental branch of mathematics that deals with the study of shapes, sizes, and positions of objects. It is a vast and fascinating field that has numerous applications in various aspects of our lives, from architecture to engineering. One of the essential concepts in geometry is the understanding of complementary and supplementary angles. In this article, we will delve into the world of angles and explore five ways to master complementary and supplementary angles.
What are Complementary and Supplementary Angles?
Before we dive into the strategies for mastering complementary and supplementary angles, let’s first define what they are.
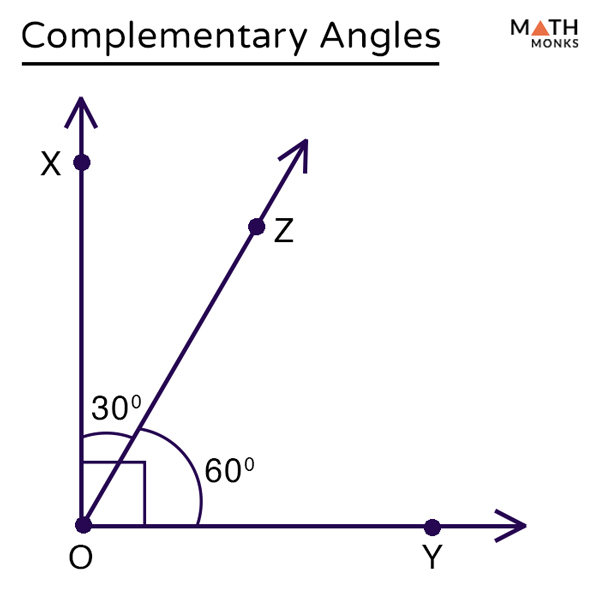
Complementary angles are two angles whose sum is equal to 90 degrees. For example, if we have two angles, 30 degrees and 60 degrees, they are complementary because their sum is 90 degrees.
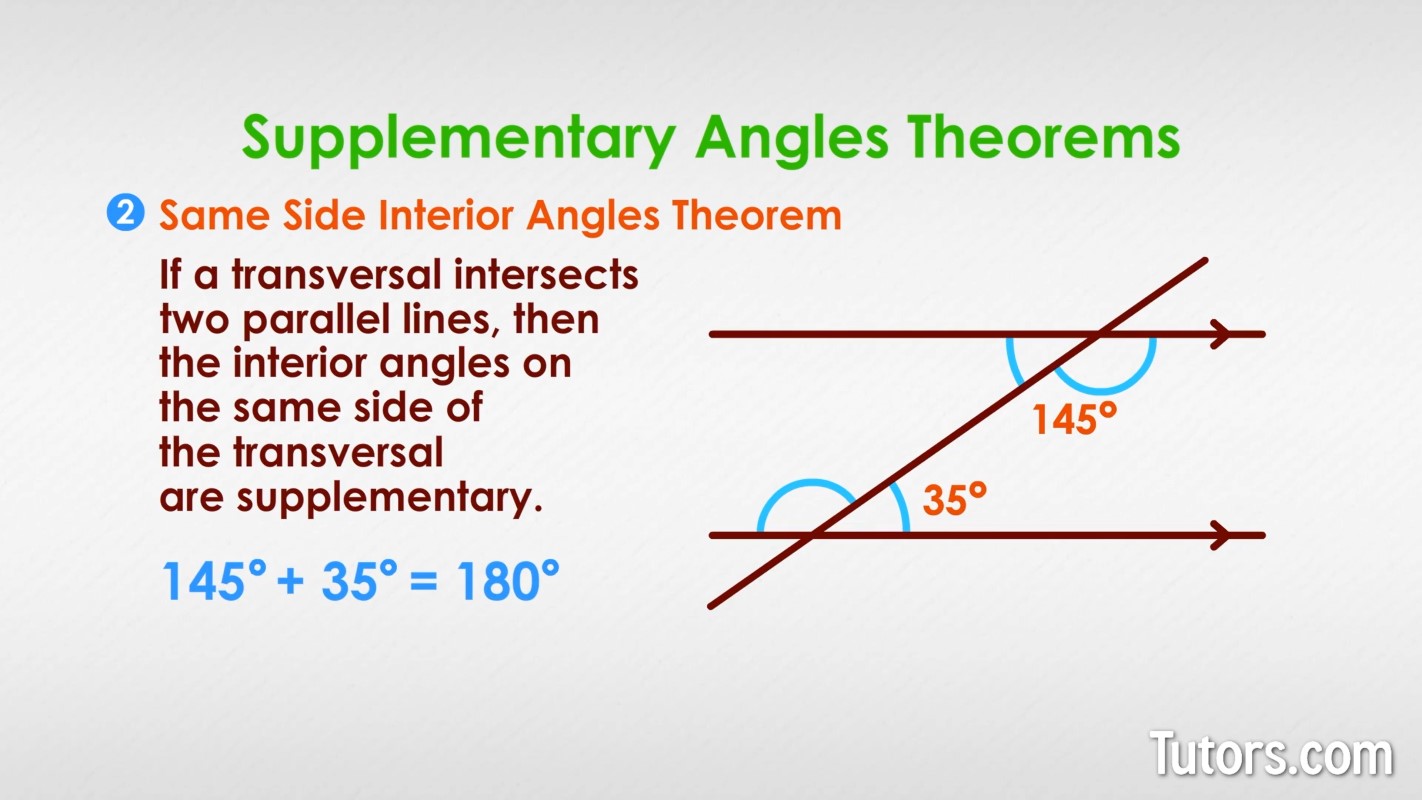
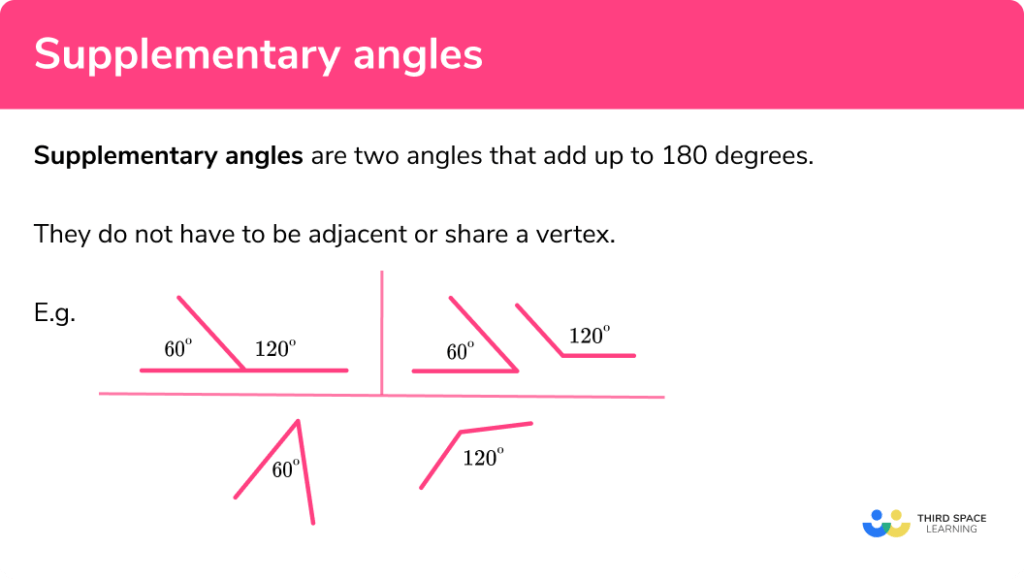
Supplementary angles, on the other hand, are two angles whose sum is equal to 180 degrees. For instance, if we have two angles, 120 degrees and 60 degrees, they are supplementary because their sum is 180 degrees.
5 Ways to Master Complementary and Supplementary Angles
Now that we have a clear understanding of complementary and supplementary angles, let’s explore five strategies to help you master them.
1. Understand the Relationship Between Complementary and Supplementary Angles
To master complementary and supplementary angles, it’s essential to understand the relationship between them. Complementary angles are like two pieces of a puzzle that fit together to form a right angle (90 degrees). Supplementary angles, on the other hand, are like two pieces of a puzzle that fit together to form a straight angle (180 degrees).
By recognizing this relationship, you can easily identify complementary and supplementary angles in various geometric shapes.
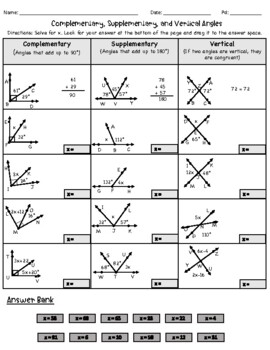
2. Use Visual Aids to Reinforce Your Understanding

Visual aids such as diagrams, charts, and graphs can help reinforce your understanding of complementary and supplementary angles. By visualizing the relationships between angles, you can better comprehend how they work together.
Here’s an example of a table that illustrates the relationship between complementary and supplementary angles:
| Angle 1 | Angle 2 | Complementary/Supplementary |
|---|---|---|
| 30 degrees | 60 degrees | Complementary |
| 120 degrees | 60 degrees | Supplementary |

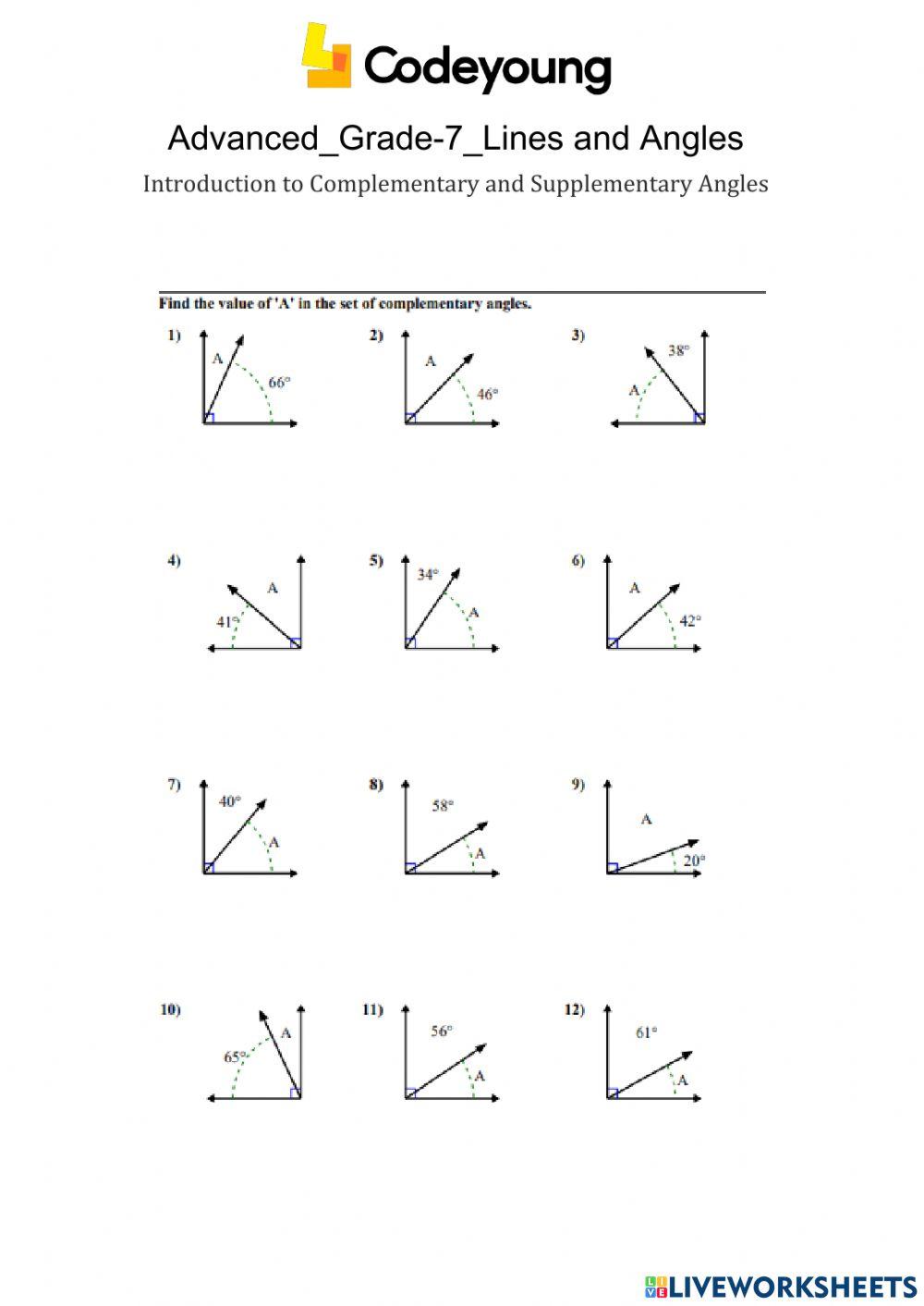
3. Practice, Practice, Practice!

Practice is key to mastering complementary and supplementary angles. The more you practice, the more comfortable you’ll become with identifying and working with these angles.
Here are some practice exercises to get you started:
- Identify the complementary angle of 45 degrees.
- Find the supplementary angle of 135 degrees.
- If two angles are complementary, and one angle is 30 degrees, what is the other angle?
4. Learn to Identify Complementary and Supplementary Angles in Real-World Scenarios

Complementary and supplementary angles are not just limited to geometric shapes; they can be found in real-world scenarios as well. By learning to identify these angles in everyday situations, you can develop a deeper understanding of their significance.
For example, when building a house, architects use complementary angles to ensure that the roof is at a 90-degree angle to the walls. Similarly, when designing a bridge, engineers use supplementary angles to ensure that the bridge is stable and secure.
5. Use Online Resources to Supplement Your Learning

There are numerous online resources available that can help you master complementary and supplementary angles. Websites such as Khan Academy, Mathway, and GeoGebra offer interactive tutorials, practice exercises, and quizzes to help you reinforce your understanding of these angles.
In addition, you can also use online tools such as angle calculators and geometry software to explore and visualize complementary and supplementary angles.
📝 Note: Make sure to practice regularly and use a variety of resources to reinforce your understanding of complementary and supplementary angles.
By following these five strategies, you can master complementary and supplementary angles and develop a deeper understanding of geometry. Remember to practice regularly, use visual aids, and explore real-world scenarios to reinforce your learning.
In the end, mastering complementary and supplementary angles is not just about memorizing formulas and concepts; it’s about developing a deeper understanding of the relationships between angles and how they work together to form geometric shapes.
What is the difference between complementary and supplementary angles?
+
Complementary angles are two angles whose sum is equal to 90 degrees, while supplementary angles are two angles whose sum is equal to 180 degrees.
How can I identify complementary and supplementary angles in real-world scenarios?

+
You can identify complementary and supplementary angles in real-world scenarios by looking for relationships between angles in everyday objects and structures, such as buildings, bridges, and furniture.
What online resources can I use to practice complementary and supplementary angles?
+
There are numerous online resources available, including Khan Academy, Mathway, and GeoGebra, that offer interactive tutorials, practice exercises, and quizzes to help you reinforce your understanding of complementary and supplementary angles.



