Graham's Law of Effusion Worksheet Solutions

Understanding the principles behind the rates at which different gases effuse is essential for students in chemistry, particularly when studying gas behavior. Graham's Law of Effusion provides a straightforward, yet profound insight into this phenomenon. This blog post is dedicated to providing you with comprehensive Graham's Law of Effusion worksheet solutions, designed to clarify and reinforce your understanding of how and why gases move at different rates.
Understanding Graham's Law of Effusion

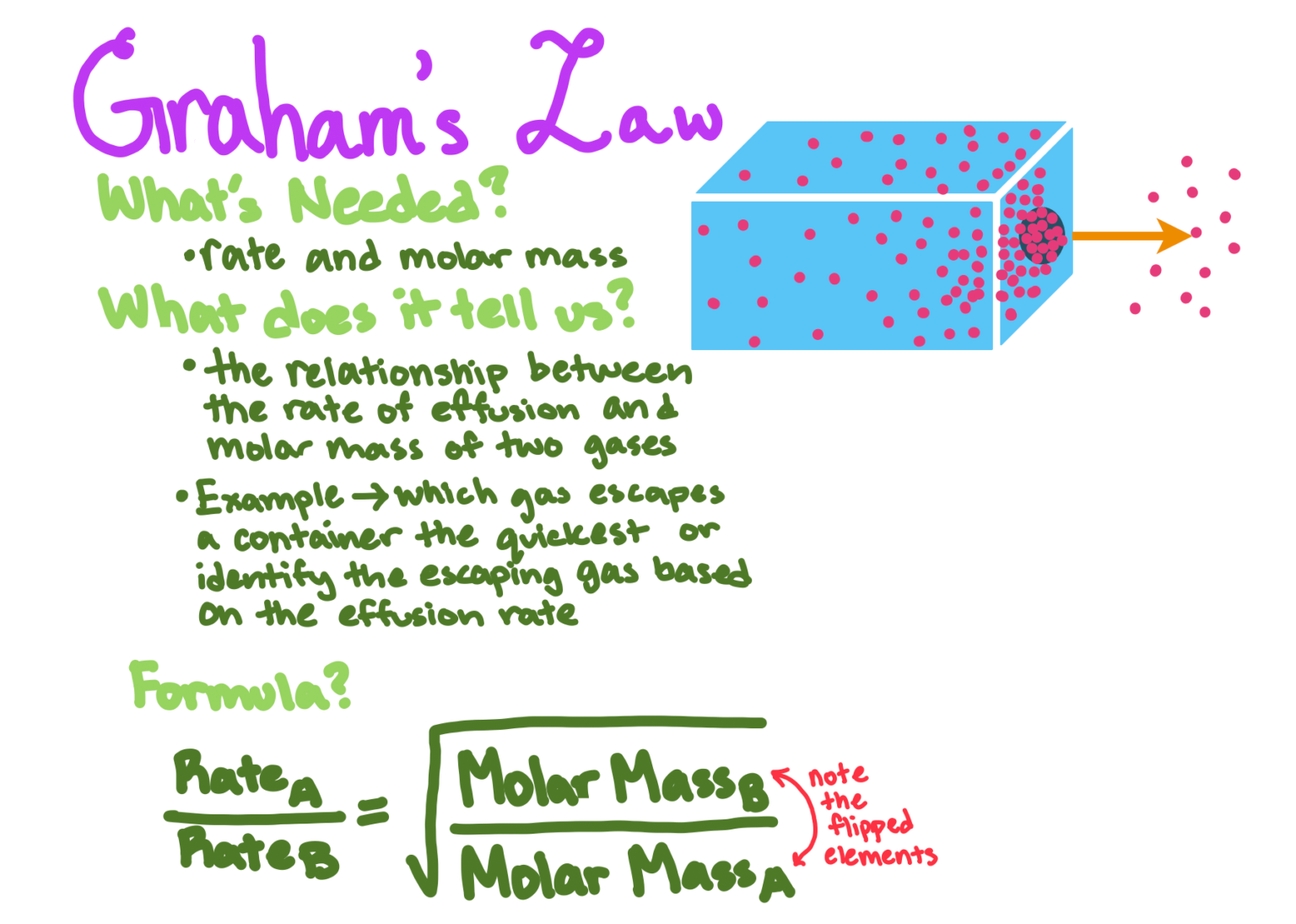
Graham's Law of Effusion states that the rate at which gases effuse is inversely proportional to the square root of their molar masses. Here's the mathematical representation of this law:
\[ Rate_1 / Rate_2 = \sqrt{M_2 / M_1} \]
- Rate_1: Effusion rate of the first gas
- Rate_2: Effusion rate of the second gas
- M_1: Molar mass of the first gas
- M_2: Molar mass of the second gas
📝 Note: This law applies under conditions where the gases behave ideally, meaning at standard temperature and pressure (STP).
Practical Applications

Graham's Law has several practical applications:
- It's used in the separation of isotopes, where lighter isotopes effuse faster.
- In gas separation processes in industries.
- To understand how different gases will behave when diffusing or effusing from a container.
Worksheet Solutions
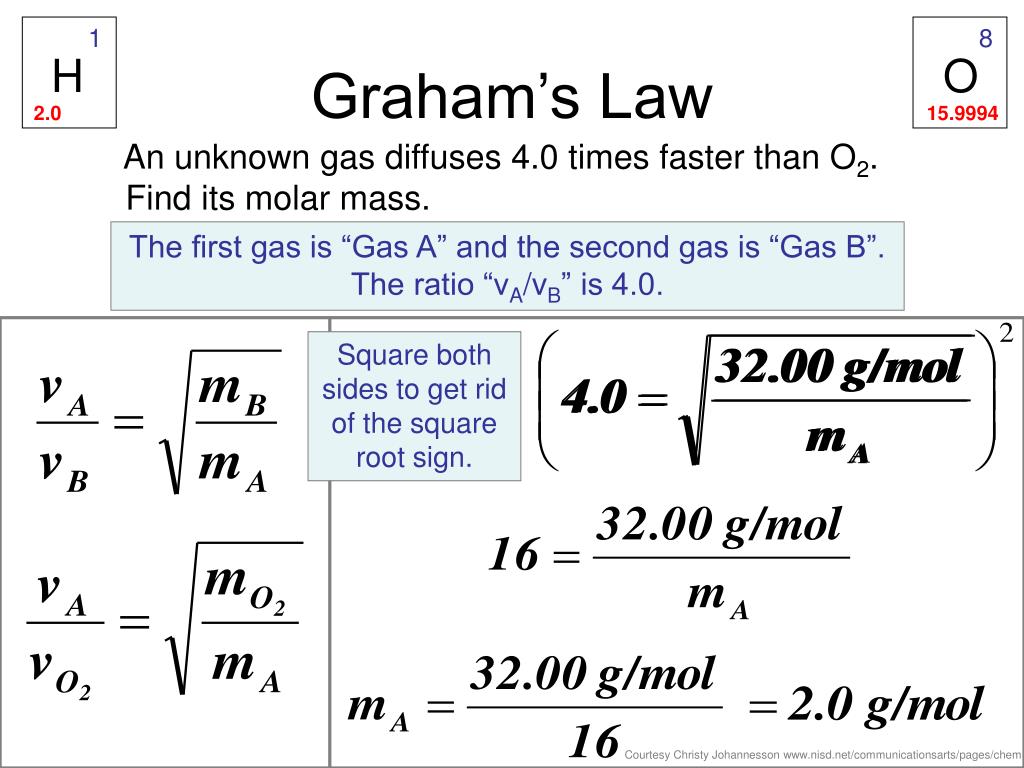
Problem 1: Effusion Rate Ratio

Given gases A and B with molar masses of 16 g/mol and 32 g/mol, respectively, calculate the ratio of their effusion rates.
- Solution:
Using Graham’s Law:
[ \text{Effusion Rate Ratio} = \sqrt{32 / 16} = \sqrt{2} \approx 1.41 ]
Therefore, gas A effuses approximately 1.41 times faster than gas B.
Problem 2: Effusion Time

How much time will it take for the same amount of helium (He) to effuse out of a container as it takes for hydrogen (H2) to effuse?
- Solution:
Given:
- Molar mass of He = 4 g/mol
- Molar mass of H2 = 2 g/mol
Using Graham’s Law:
[ t{He} / t{H2} = \sqrt{M{H2} / M{He}} = \sqrt{2 / 4} = 0.707 ]
So, helium takes approximately 70.7% of the time hydrogen takes to effuse the same amount.
Problem 3: Gas Composition

If a mixture of nitrogen (N2) and oxygen (O2) effuses through a pinhole, what will be the composition of the effused gases?
- Solution:
Since effusion rates are inversely proportional to the square root of molar masses:
- N2: Molar mass = 28 g/mol
- O2: Molar mass = 32 g/mol
The ratio of their rates:
[ \text{Effusion Rate Ratio} = \sqrt{32 / 28} \approx 1.071 ]
Thus, the effused mixture will contain 7.1% more nitrogen than oxygen.
🔬 Note: This problem assumes that both gases are at the same temperature and pressure, and the effusion is complete enough to measure composition changes.
Summary of Key Points
Throughout this blog post, we’ve explored:
- The Graham’s Law of Effusion and its mathematical expression.
- Practical applications of the law in various fields.
- Worksheet solutions that illustrate how to apply Graham’s Law in different scenarios.
The study of effusion rates not only deepens our understanding of gas behavior but also has significant industrial implications, from isotopic separation to gas purification. By mastering the calculations and applications of Graham's Law, students and professionals can better predict and manage gas interactions in various systems.
Why does effusion rate depend on molar mass?

+
Since effusion rate is directly related to molecular velocity, and the velocity of gas molecules is inversely proportional to the square root of their molar masses, lighter molecules move faster, and thus effuse faster.
How can Graham’s Law be applied in real-world scenarios?

+
Graham’s Law is useful in processes like isotope separation in nuclear reactors, air pollution control, and pharmaceutical manufacturing where controlling the rates of gas diffusion is crucial.
Does Graham’s Law work under all conditions?

+
Graham’s Law assumes ideal gas behavior, which holds true at STP (Standard Temperature and Pressure) or low pressures. At high pressures or extreme temperatures, deviations from ideal behavior can affect the law’s accuracy.