Graham's Law of Effusion Made Simple: Worksheet Guide

Understanding Graham's Law of Effusion can seem daunting at first, but with the right approach, it can be broken down into digestible parts. In this guide, we'll go through a worksheet that simplifies Graham's Law of Effusion, providing you with a clear understanding of how different gases effuse or diffuse through an aperture into a vacuum under identical conditions of temperature and pressure. Whether you're a student, a teacher, or someone curious about gas behavior, this guide will help clarify this essential principle of chemistry.
What is Graham’s Law of Effusion?

Before diving into the worksheet, let’s briefly revisit what Graham’s Law states:
- Definition: Graham’s Law of Effusion describes the relationship between the rate of effusion (or diffusion) of a gas and its molecular mass.
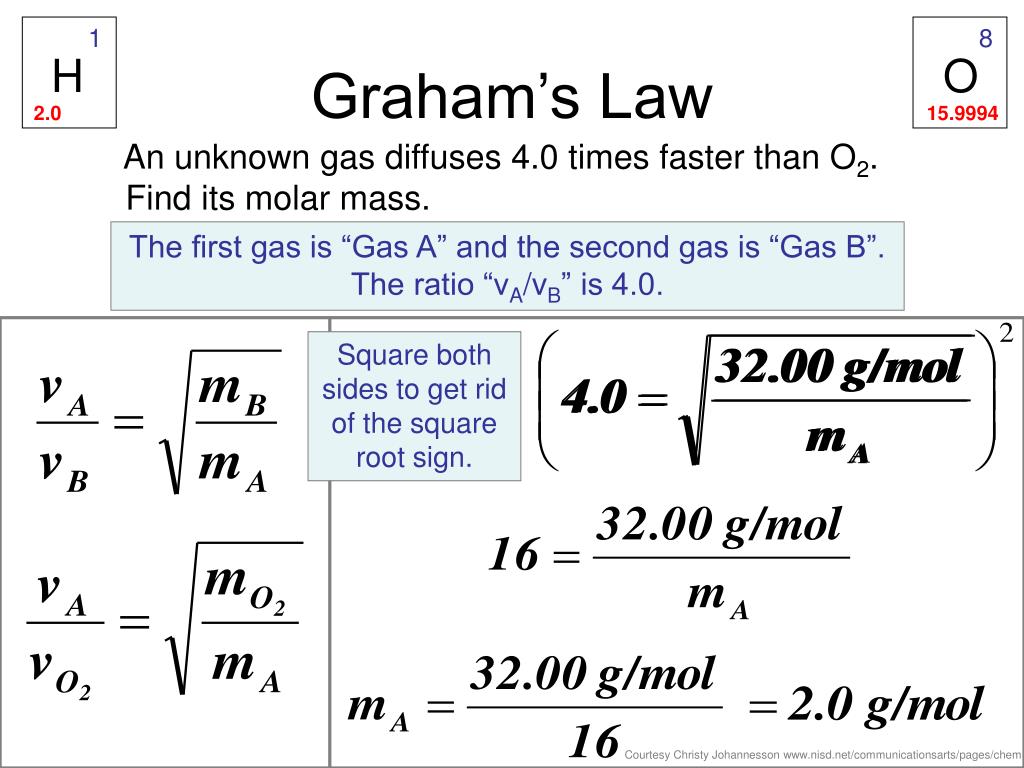
- Formula: The rate of effusion of a gas (r) is inversely proportional to the square root of its molar mass (M): r ∝ 1/√M.
- Comparative Form: For two gases A and B, (rA/rB) = √(MB/MA).
The Graham’s Law Worksheet Guide
Here’s how you can work through a worksheet to understand Graham’s Law better:
1. Identify the Molecular Masses

The first step involves knowing the molecular mass of the gases in question. Remember that:
- Molecular mass can be found by adding up the atomic masses from the periodic table.
- If a compound is given instead of an element, ensure you account for all the atoms present.
🔍 Note: Always use the molar mass of the entire molecule, not just the atomic weight of its elements, for calculations involving compounds.
2. Set Up the Equation

When comparing the effusion rates of two gases:
| Gas A | Gas B |
|---|---|
| Rate of Effusion | Rate of Effusion |
| Molecular Mass (MA) | Molecular Mass (MB) |
| √(MB) | √(MA) |

3. Calculate and Compare

Use the equation:
- (rA/rB) = √(MB/MA)
Plug in the molar masses and solve for the ratio of rates.
4. Interpret Results

After calculating:
- Understand that the heavier gas will effuse slower than the lighter one.
- The ratio calculated indicates how many times faster or slower one gas effuses compared to another.
Advanced Considerations

Sometimes, the worksheet might delve into real-life applications or more complex scenarios:
- Temperature: If the temperature differs, the rates of effusion will change because of the change in molecular speed.
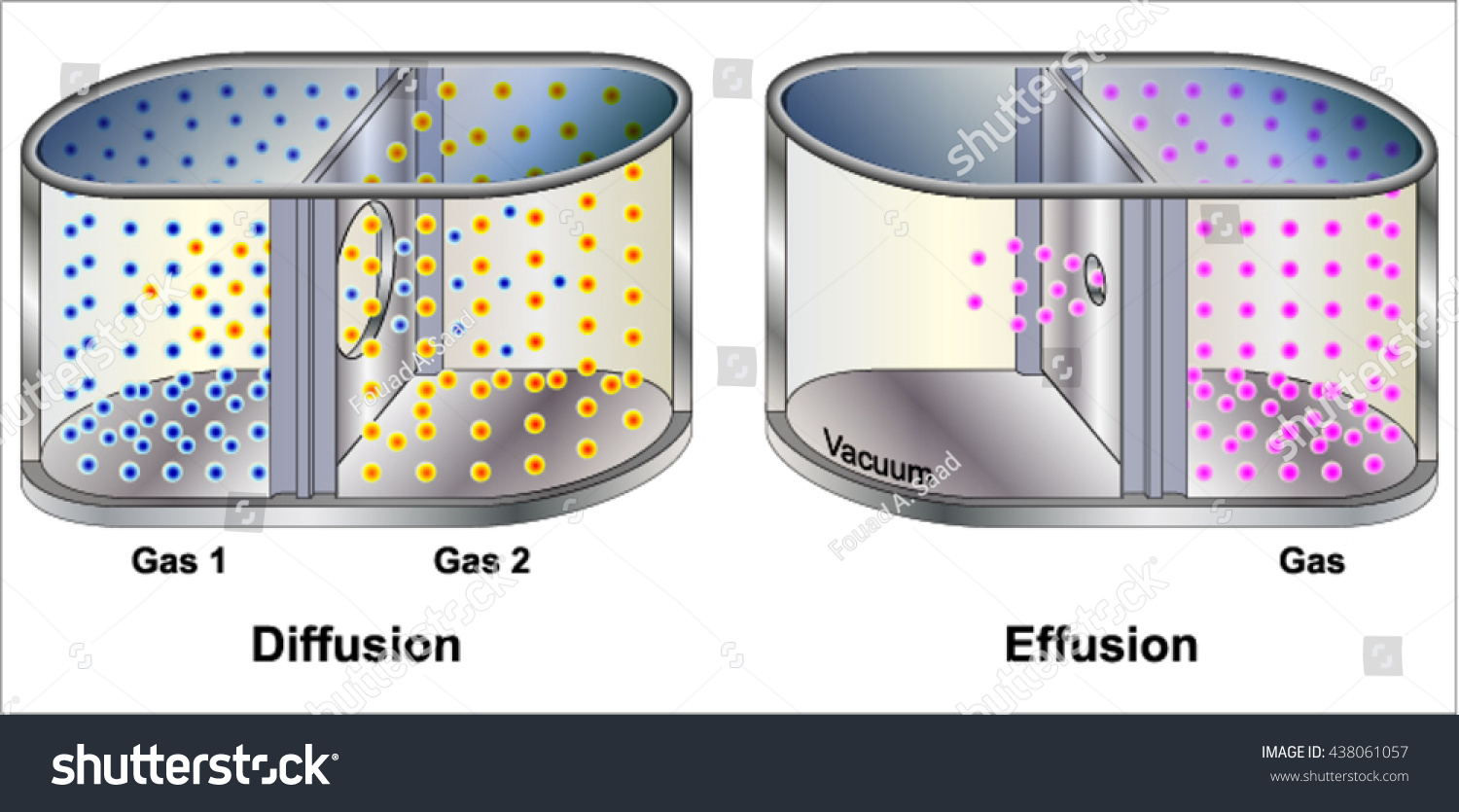
- Diffusion vs. Effusion: Distinguish between diffusion (spreading out in space) and effusion (escaping through a small hole).
- Real Gas Behavior: Although Graham’s Law applies best to ideal gases, adjustments for real gas behavior might be necessary for accurate predictions.
🔺 Note: Remember that while Graham's Law simplifies effusion, real-world factors like viscosity, molecular interactions, or high pressure can affect the rate of effusion.
In this exploration of Graham’s Law, we’ve not only gone through the basic concepts but also covered how to tackle a worksheet, interpret results, and consider advanced factors. This knowledge is not only vital for academic purposes but also for understanding various industrial processes where gas behavior plays a critical role. By mastering the nuances of this law, students and professionals can better predict and manipulate gas behavior, enhancing both safety and efficiency in applications ranging from respiratory equipment to gas separation technologies.
What is the difference between effusion and diffusion?

+
Effusion is the process where a gas escapes through a small opening into a vacuum, while diffusion refers to the spreading of gas molecules through another medium, either gas or another substance, due to random molecular motion.
How does temperature affect Graham’s Law?

+
Temperature directly affects the speed at which gas molecules move. According to kinetic theory, as temperature increases, the average kinetic energy of the molecules increases, leading to faster effusion rates.
Is Graham’s Law applicable to all gases?
+
Graham’s Law is primarily applicable to ideal gases where intermolecular forces are negligible. Real gases deviate from ideal behavior, but Graham’s Law still provides a useful approximation in many practical situations.