Geometry Transformation Composition Worksheet Mastery Guide
Learning about geometry transformation composition can be a fascinating and enriching journey for anyone keen on mathematics or visual arts. Whether you're studying for school, brushing up for teaching, or just exploring math for fun, understanding how transformations combine in geometry offers a deeper insight into the beauty of shapes and patterns. This guide aims to provide a comprehensive understanding of composition in geometric transformations through a series of meticulously designed worksheets.
Understanding Transformations
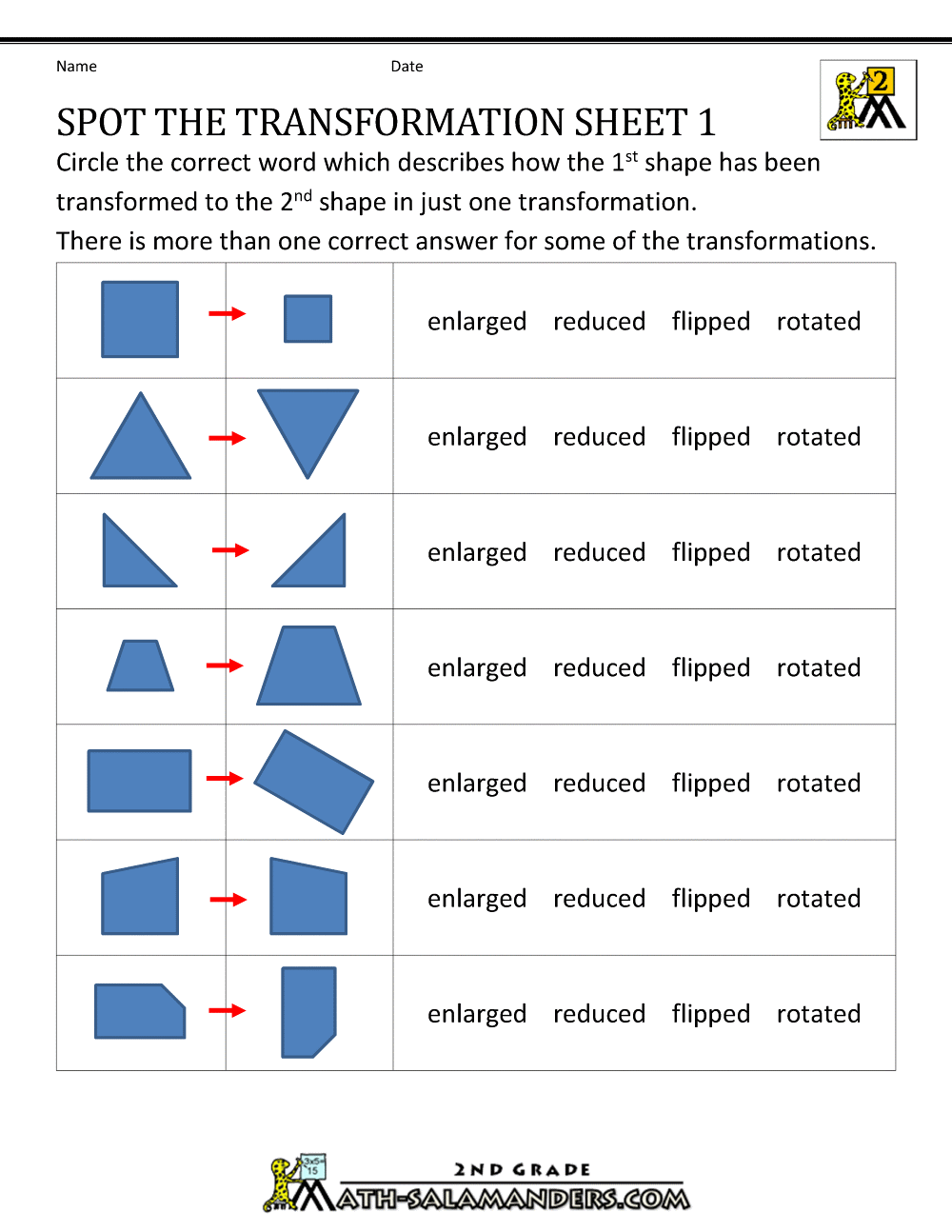
Before diving into composition, let's briefly review the key types of geometric transformations:
- Translation - moving every point of a shape the same distance in a given direction.
- Reflection - flipping a shape over a line called the axis of symmetry.
- Rotation - rotating a shape around a fixed point known as the center of rotation.
- Dilation - resizing a shape with respect to a center point, maintaining the shape's proportions.
🔄 Note: Understanding each transformation individually will help you better grasp their interactions when composed.
Composing Transformations

When we talk about composition of transformations, we mean applying multiple transformations one after another. Here's how it works:
- Perform the first transformation.
- Using the result, apply the second transformation.
- Repeat as necessary for subsequent transformations.
The order in which these transformations are performed is crucial because geometry does not generally commute with transformations. Here's how you might approach teaching or learning this:
Step-by-Step Guide to Composition Worksheets

-
Identify the Shape
Start with identifying the shape to be transformed. Label the vertices for clarity.
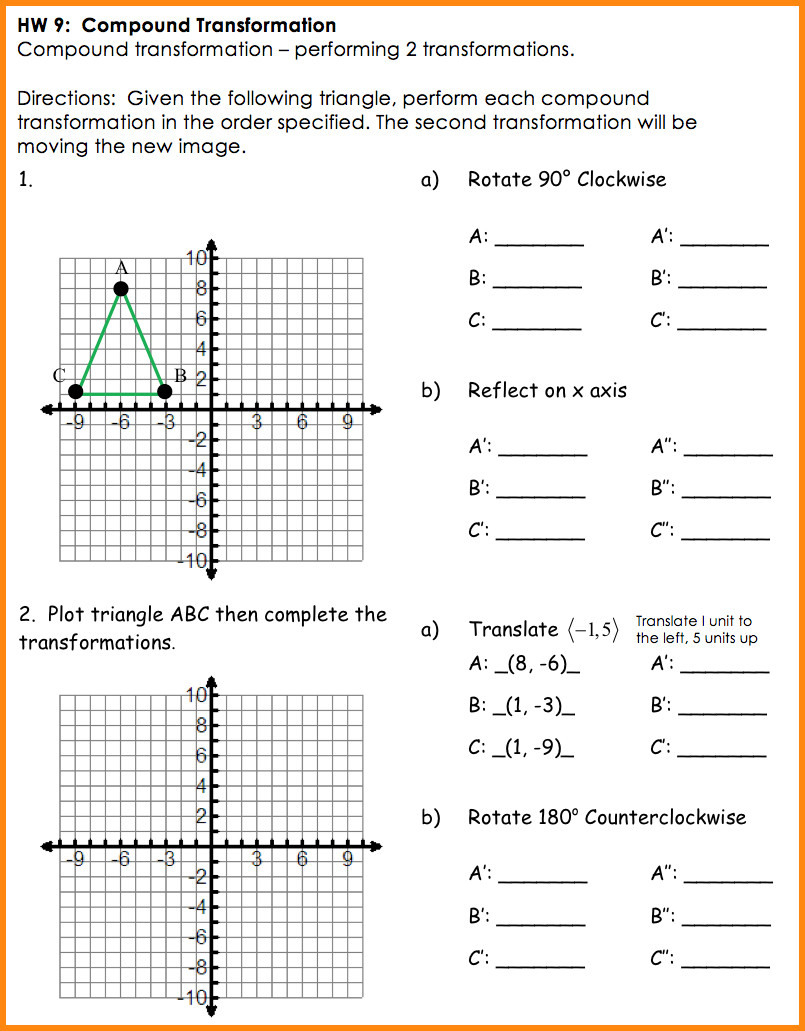
Shape Vertices Triangle A, B, C Rectangle W, X, Y, Z Hexagon A, B, C, D, E, F 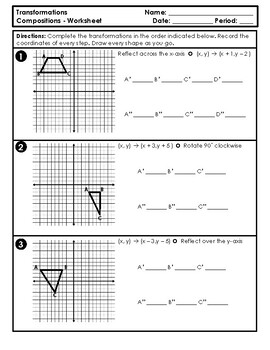
📚 Note: Make sure students can clearly identify and name points for transformations.
-
Select Transformations
Choose transformations in the order they are to be applied. Example: Rotation → Translation → Reflection.
-
Apply Each Transformation
- Perform the first transformation. Draw or describe the result.
- On the result from the first transformation, apply the second one. Continue for all selected transformations.
-
Summarize Results
After applying all transformations, summarize the final position or appearance of the shape.
📝 Note: Encourage learners to use coordinates or graphical methods to track changes in the shape's position.
-
Analyze the Composition
Reflect on how the order of transformations affects the final outcome. Was there a significant difference if the order was changed?
-
Challenge
Challenge students to reverse-engineer a transformation sequence from a final shape back to the original, or create new sequences with different effects.
Common Mistakes in Transformation Composition
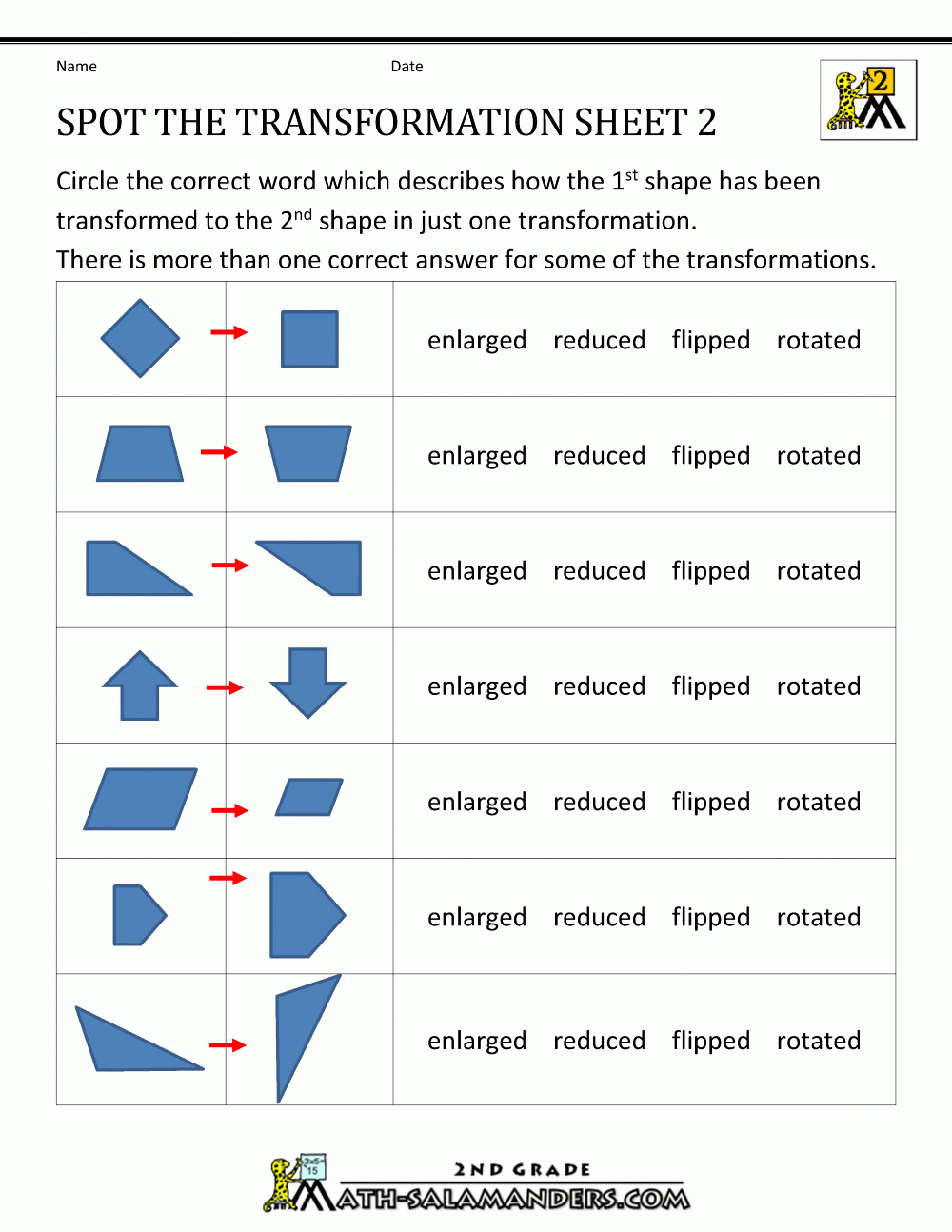
Here are some common errors to watch out for:
- Order Mistake: Performing transformations in the wrong order can lead to different results.
- Scaling Errors: Incorrectly applying dilation can distort the shape or size wrongly.
- Reference Points: Forgetting to use the correct point for rotation or reflection.
🚫 Note: Reinforce the importance of transformation order to avoid confusion.
Worksheet Design Tips

To create effective geometry transformation composition worksheets:
- Use visuals: Include diagrams and grid paper to help students visualize transformations.
- Progressive difficulty: Start with simple compositions and gradually increase complexity.
- Real-world applications: Show how transformations are used in areas like art, computer graphics, or architecture.
- Clear instructions: Make sure every step is clearly explained to avoid confusion.
Practical Applications

Transformations in geometry are not just theoretical; they have practical applications:
- Computer graphics: Transforming images and rendering 3D scenes.
- Manufacturing: Designing parts with precise transformations.
- Robotics: Moving robotic arms or navigating autonomous systems.
Understanding composition can help in creating complex movements and designs through simpler transformations.
Reflecting on our journey through the intricacies of geometric transformation composition, we can appreciate how these fundamental concepts in mathematics are not only educational but also immensely practical. Through careful study and practice, anyone can master this fascinating aspect of geometry, enriching their mathematical toolkit and perhaps even their artistic or technological endeavors.
Why is the order of transformations important in composition?

+
The order is crucial because transformations in geometry do not commute; that is, applying transformations in different orders can result in different final shapes or positions. This is because each transformation sets the stage for the next one, affecting how subsequent transformations will alter the figure.
Can you compose all types of transformations?

+
Yes, you can compose any combination of translations, reflections, rotations, and dilations. However, the complexity increases with each added transformation, and you might need to pay attention to how they interact with each other, especially with scaling and rotation.
How can I check my work when doing transformation compositions?

+
One effective way to verify your work is to draw each step on graph paper, ensuring each transformation’s result is correct before moving to the next. Additionally, reversing the transformations to return to the original shape can confirm accuracy.
Are there any software tools for practicing transformation composition?

+
Yes, various educational math software and websites offer tools for practicing geometry, including Desmos, GeoGebra, or even some online platforms that allow you to manipulate shapes through transformations interactively.



