Geometry Reflections Worksheet: Simplify Your Learning

Geometry is a fascinating branch of mathematics that deals with the shape, size, position, and properties of figures and spaces. One fundamental concept within this vast field is reflection, a type of transformation where a geometric figure is mirrored over a line, called the line of reflection or axis. This worksheet aims to delve into the art of reflections, simplifying the learning process for students through comprehensive exercises and examples.
Understanding Reflection in Geometry

Reflection in geometry refers to the process of flipping a shape over a line to create a mirror image of the original figure. This can involve points, lines, shapes, or complex patterns:
- A point: Reflecting a point across a line results in another point that is equidistant from the line.
- A line: A line segment or an entire line can be reflected to form its symmetrical counterpart.
- A shape: An entire shape like a triangle or a polygon can be reflected to create an image that appears to be looking into a mirror.

Practical Exercises for Reflection

Reflecting Points
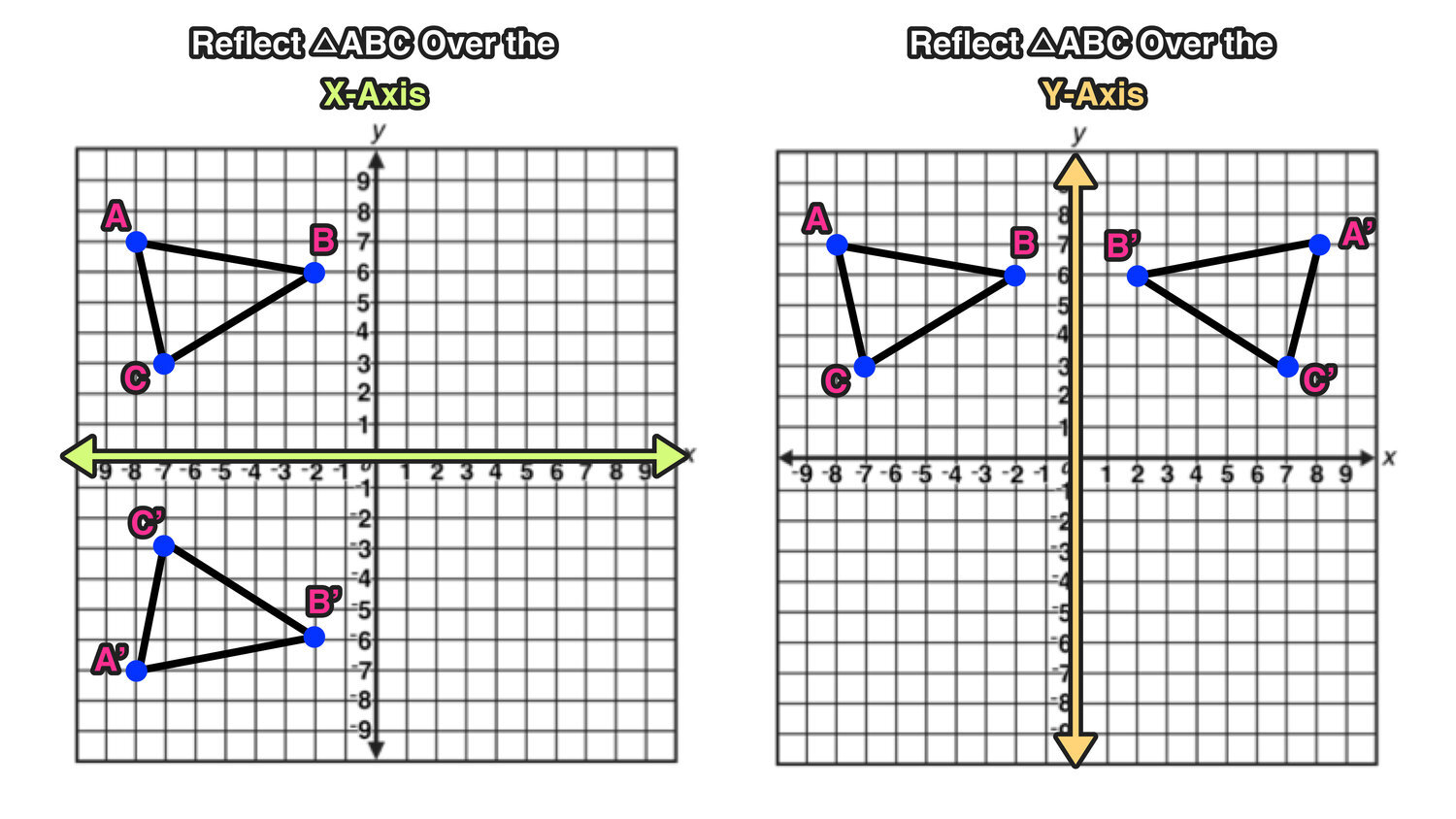
Begin by reflecting points:
- Identify a point on a coordinate plane.
- Choose the line of reflection, such as the x-axis, y-axis, or another line.
- Calculate the new coordinates of the reflected point.
📝 Note: Reflecting a point (a, b) over the x-axis gives (a, -b).
Reflecting Lines and Shapes

Once comfortable with points, extend this understanding to lines and shapes:
- Reflect a line segment or shape over a line and draw the resulting figure.
- Use a ruler to ensure accurate reflections.
- Check for symmetry in the reflected shape.
Properties and Rules of Reflection

Here are key properties to keep in mind when dealing with reflections:
- Symmetry: The original figure and its reflection will have line symmetry. The line of reflection serves as the axis of symmetry.
- Distance: The distance from each point of the figure to the line of reflection is the same as the distance from its reflection to the line.
- Orientation: The orientation of the figure changes. For instance, a right-handed figure will become left-handed after reflection.
| Shape | Original Coordinates | Line of Reflection | Reflected Coordinates |
|---|---|---|---|
| Point | (3, 4) | y-axis | (-3, 4) |
| Line segment | (1,1) to (3,3) | x-axis | (1,-1) to (3,-3) |
| Triangle | (2,2), (4,6), (6,4) | y = x | (2,2), (6,4), (4,6) |

Applying Reflections in Real Life

Reflections are not just abstract mathematical concepts; they have practical applications:
- In design, understanding reflection symmetry can help create balanced and visually appealing compositions.
- In physics, reflections are used to explain light behavior or how sound waves might interact with different surfaces.
- In computer graphics and video games, reflections are simulated to create realistic visuals.
💡 Note: In design, reflective symmetry can often enhance aesthetic appeal and create visually pleasing patterns.
Enhancing Learning with Interactive Tools

To deepen your understanding of reflections, interactive tools can be incredibly beneficial:
- Use dynamic geometry software to reflect shapes and observe the transformation in real time.
- Online reflection simulators allow for experimentation with different lines of reflection.
- Video tutorials provide visual explanations, making complex concepts more accessible.
🔧 Note: Many educational platforms offer free tools for geometric transformations which can aid in visualizing and understanding reflections better.
Understanding reflections in geometry not only fosters a deeper appreciation for the subject but also equips students with the ability to apply these concepts in various fields. Whether in art, science, or technology, reflections illustrate how fundamental geometric principles can have widespread utility. This worksheet has explored reflections through exercises, rules, and real-world applications, making the learning process more dynamic and engaging. By practicing these techniques, students not only master reflection but also unlock a broader understanding of symmetry and transformation in the world around us.
What is the line of reflection?
+
The line of reflection is an axis, often a line or a coordinate axis, over which a figure or point is reflected to create its mirror image.
How do you reflect a shape over the y-axis?

+
To reflect a shape over the y-axis, for each point in the shape with coordinates (x, y), find the new coordinate by changing the sign of the x-value, resulting in (-x, y).
Can reflections change the orientation of an object?

+
Yes, reflections change the orientation of an object. If an object is considered right-handed before reflection, it will become left-handed after being reflected.
Are there any online tools to practice geometric reflections?

+
Yes, there are numerous interactive geometry tools available online that provide dynamic simulations for practicing geometric reflections.
Why is understanding reflection important in geometry?

+
Understanding reflection is crucial because it’s one of the basic transformations that help in understanding symmetry, coordinate systems, and spatial relationships, which are fundamental in various fields beyond mathematics.



