Geometry 3.5 Worksheet Answers

Understanding Geometry 3.5: Worksheet Answers
Geometry is a foundational subject in mathematics that helps students grasp concepts of shapes, dimensions, and space. In this blog post, we’ll delve into the answers for Geometry Worksheet 3.5, providing detailed explanations and steps to solve common geometric problems.
What are the Main Topics in Geometry 3.5?

Geometry 3.5 often includes:
- Bisectors, Medians, and Altitudes: Learning about different lines that can be drawn within triangles.
- Proving Congruence: Theorems like ASA, SSS, and SAS to show that triangles are congruent.
- Midpoints and Medians: Calculations and proofs involving midpoints of segments and medians of triangles.
- Properties of Parallelograms: Understanding how diagonals, opposite sides, and angles relate in a parallelogram.
Each of these topics has its own set of problems that can be challenging yet rewarding to solve. Here, we’ll focus on common problems and provide step-by-step solutions.
Problem 1: Triangle Congruence


Problem: Given triangles ABC and DEF with the following measurements: - AB = DE - AC = DF - ∠A = ∠D
Prove that △ABC ≡ △DEF using the ASA postulate.
Solution:
State the given information:
- AB = DE
- AC = DF
- ∠A = ∠D
Identify the congruence postulate:
Since we know two sides and the included angle for both triangles, we can use the ASA (Angle-Side-Angle) postulate.Apply ASA postulate:
By the ASA Postulate, if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent. Thus:- ∠A = ∠D
- Side AC = DF
- Side AB = DE
- △ABC ≡ △DEF
📚 Note: When proving congruence, always start by identifying what given information matches which postulate or theorem.
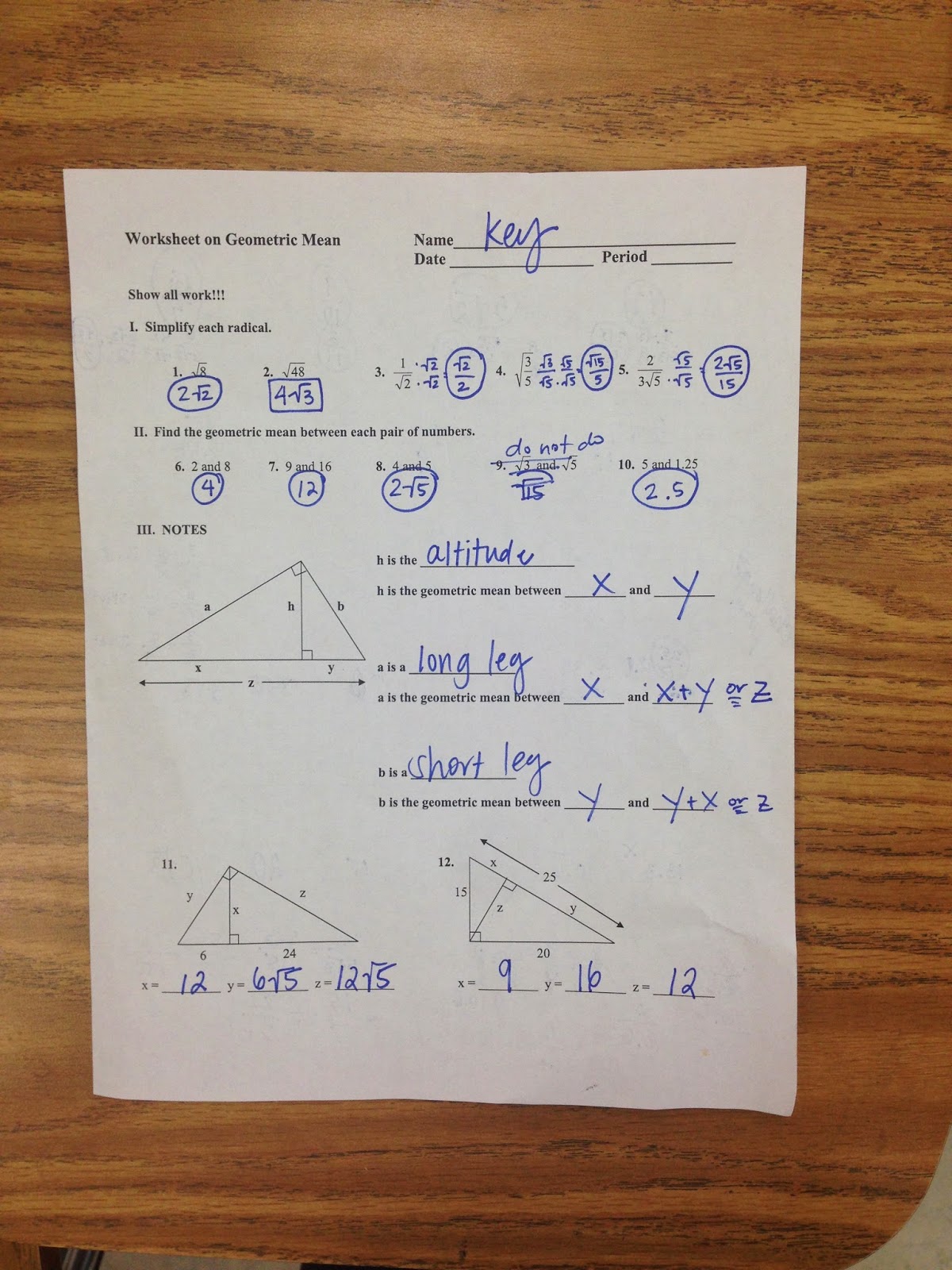
Problem 2: Bisectors and Medians

Problem: In triangle PQR, point M is the midpoint of PR, and QM is the median. Find the coordinates of point M if:
- P(2, 6)
- R(8, -4)
- Q(5, 1)
Solution:
Find the midpoint M:
Midpoint formula: M = ((x1 + x2)/2, (y1 + y2)/2)- For PR:
- M = ((2 + 8)/2, (6 + (-4))/2) = (5, 1)
- For PR:
Verify M as the midpoint of PR:
Since QM is the median, Q must lie on this line, confirming the calculations.
| Step | Calculation |
|---|---|
| 1 | Midpoint of PR |
| 2 | Verify median QM |

Problem 3: Properties of Parallelograms

Problem: In parallelogram ABCD, AB = 6, BC = 10, and the diagonals intersect at point O. Find the length of AO if the diagonals are bisected at O.
Solution:
Understand diagonal properties:
- The diagonals of a parallelogram bisect each other.
Calculate diagonal length:
- Let AO = x
- Therefore, AC = 2x
- By the Pythagorean Theorem in △AOB (assuming AO bisects perpendicularly):
- AC² = AB² + BC²
- (2x)² = 6² + 10²
- 4x² = 36 + 100
- 4x² = 136
- x² = 34
- x = √34
As you navigate through the geometric world of triangles, congruence, bisectors, medians, and parallelograms, these solutions should provide you with the clarity needed to tackle similar problems in your geometry studies. Remember, the key to mastering geometry lies in understanding the relationships between the elements of shapes and applying theorems correctly.
Final Thoughts:
Geometry, with its visual puzzles and logical steps, offers a unique way to understand the structure of our world. Through the problems and solutions provided here, we’ve covered essential techniques that will not only help in solving your worksheet but also in developing a deeper appreciation for spatial reasoning and mathematical proofs. Keep practicing, and soon, these geometric concepts will become second nature.
What is the difference between a median and an altitude of a triangle?
+
A median in a triangle connects a vertex to the midpoint of the opposite side, while an altitude is a line segment from a vertex perpendicular to the line containing the opposite side.
How can we prove that triangles are congruent?

+
Triangles can be proven congruent by matching their sides and angles using postulates like SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), or HL (Hypotenuse-Leg for right triangles).
Why do the diagonals of a parallelogram bisect each other?

+
In a parallelogram, the diagonals bisect each other due to the symmetry of the shape. This property is derived from the fact that opposite sides are congruent and parallel, ensuring that the diagonals intersect at their midpoints.