Geometry 11.1 Worksheet Answers: Your Guide to Success

Geometry, often considered one of the most visually compelling branches of mathematics, offers a unique perspective into the world around us. It's not just about shapes, angles, and theorems; it's about understanding spatial relationships and applying mathematical concepts to solve real-world problems. Chapter 11.1 in your Geometry textbook is dedicated to Points, Lines, Planes, and Angles. For many students, grasping these foundational concepts can be both exciting and challenging. This blog post aims to provide a comprehensive guide to help you navigate through the worksheet answers of Chapter 11.1, ensuring you're on the right path to success.
Understanding Points, Lines, and Planes
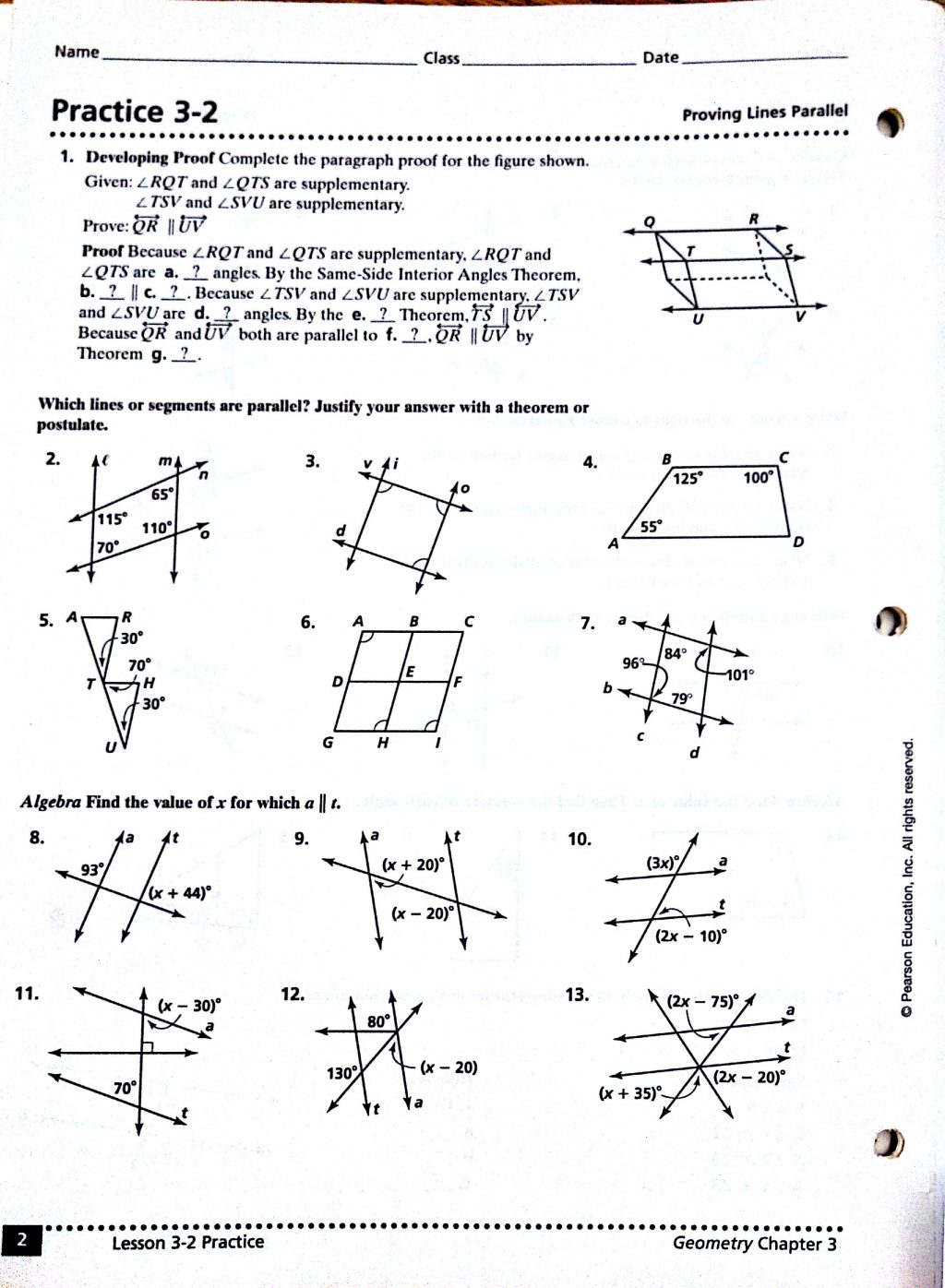

Before diving into the worksheet answers, it's crucial to have a firm grip on the basic definitions:
- Point: A location in space without any dimensions, depicted as a dot.
- Line: A one-dimensional figure that extends infinitely in both directions.
- Plane: A flat, two-dimensional surface that extends infinitely in all directions.
Key Concepts

- Collinear points
- Coplanar points
- Intersecting lines
- Parallel lines
Understanding these concepts is fundamental to answering worksheet questions accurately.
Chapter 11.1 Worksheet: Detailed Answers

Here, we'll go through each question type found in Chapter 11.1, providing step-by-step solutions and important notes to enhance your understanding:
1. Identifying Points, Lines, and Planes

- Question: List three points that lie on the same line.
- Answer: Look for three points that are collinear. For example, in the provided figure, points A, B, and C might lie on line m.
🔍 Note: Always ensure you check the diagram for collinearity or coplanarity before answering these questions.
2. Angles and Their Relationships
- Question: Identify all pairs of vertical angles in the diagram.
- Answer: Vertical angles are formed when two lines intersect. Look for angles that are opposite each other at the intersection. For example, if lines AB and CD intersect at point O, angles AOC and BOD, and angles AOD and BOC are vertical angles.
3. Angles Formed by Intersecting Lines
| Question Type | Example Question | Answer |
|---|---|---|
| Linear Pair | Are angles AOB and BOC a linear pair? | Yes, if line AB and BC form a straight line at point O, these angles are adjacent and their sum is 180°. |
| Adjacent Angles | Identify the pairs of adjacent angles in the given diagram. | Adjacent angles share a common vertex and side but do not overlap. Look for pairs like AOC and BOC. |
4. Properties of Parallel Lines

- Question: If line l and m are parallel, and t is a transversal, identify all corresponding angles.
- Answer: Corresponding angles are in the same relative position at each intersection of the transversal with the parallel lines. Examples include angles formed by line t intersecting lines l and m at points A and B, respectively. Corresponding angles would be AOA’ and BOB’.
Wrap-Up

Having gone through the detailed answers for Chapter 11.1, you should now have a clearer understanding of how to approach geometry problems. The concepts of points, lines, planes, angles, and their relationships are not only fundamental in geometry but also in understanding spatial reasoning. Whether you’re calculating the angles in a complex diagram or trying to find parallel lines, the key is to recognize the patterns and apply the appropriate geometric principles.
Remember, geometry is about seeing and understanding the world through the lens of shapes and structures. By mastering the basics, you're setting yourself up for success in not just this chapter but the entire geometry curriculum.
💡 Note: Regular practice with diagrams and real-world examples will solidify your understanding and help in applying these principles effectively.
What if I struggle with visualizing points, lines, and planes?
+
Use physical models or software programs that allow you to manipulate geometric shapes in 3D space. This hands-on approach can enhance your understanding of spatial relationships.
How can I remember the properties of parallel lines?

+
Create mnemonic devices or visualize the properties with real-world examples. For instance, think of railway tracks or road markings for parallel lines, which will help you remember corresponding, alternate, and consecutive interior angles.
Can I use formulas for angle calculations?

+
Yes, formulas for angle calculations are beneficial. Understand and remember the formulas for supplementary angles (180°), complementary angles (90°), and vertical angles, which are congruent.



